SUMMARY
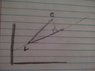
The discussion focuses on finding the point d on the line l that is closest to point c (1,1,7) using vector projections in three-dimensional space. The parametric equation of line l is given as x=2+t, u=3+2t, z=5+3t, with the angle between the vector from point c to line l being 36.7 degrees. The closest distance from point c to line l is determined to be 3 units, while the distance along the line is 4 units. The coordinates of the closest point on line l are calculated by adjusting the parameter t based on the direction vector derived from the parametric equation.
PREREQUISITES
- Understanding of three-dimensional vectors
- Knowledge of parametric equations of lines
- Familiarity with vector projections and dot products
- Basic trigonometry, specifically involving right triangles
NEXT STEPS
- Learn about vector projection techniques in three dimensions
- Study the derivation and application of parametric equations for lines
- Explore the relationship between angles and distances in vector geometry
- Investigate the use of direction vectors in determining closest points on lines
USEFUL FOR
Students studying vector mathematics, particularly in three-dimensional geometry, as well as educators looking for examples of vector projections and parametric equations in practical applications.