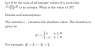Find |S|: How to Calculate Sum of Integer Values of n

[Greychu]

Homework Statement

Let S be the sum of all integer values of n such that \frac {n^2+12n-43} {n+6} is an integer. What is the value of |S|.

Homework Equations

Since it's sum, S = \frac {n} {2} \ (2a+(n-1)d) where a is the first term.
The \frac {n^2+12n-43} {n+6} = x, where x is an integer

The Attempt at a Solution

\frac {n^2+12n-43} {n+6}= x
{n^2+(12-x)n-43-6x} = 0

basically I have no idea "Let S be the sum of all integer values of n" means?
Is it means that S = n or otherwise? Need clarification for this.

 

[Joffan]

You need to find out for what values of $n$ the expression $\frac {n^2+12n-43} {n+6}$ is an integer.

It's not an arithmetic progression.

Try defining $m=n+6$ and then express $n^2+12n-43$ in terms of $m$.

 

[HallsofIvy]

I would complete the square in the numerator. From that it turns out that the fraction is an integer for only a very small number of values of n!​

 

[Greychu]

I think I got it by completing the square.
it will becomes \frac {(n+6)^2 - 79}{n+6}

Since 79 is prime number,
Solving n + 6 = ± 1 and n + 6 = ± 79 will gives rise to 4 integers, which is -5, -7, 73 and -85.
Hence, |S| = |-5-7+73-85| = 24

Thanks for pointing out the completing the square. It helps.