betaleonis
- 8
- 0
Homework Statement
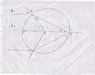
A ray of light incident on a glass sphere (refractive index sqrt 3) suffers total internal reflection before emerging out exactly parallel to the incident ray. What was the angle of incidence?
μ = refractive index of the glass sphere, i = angle of incidence, r = angle of refraction
Homework Equations
μ = sin i/sinr
The Attempt at a Solution
From the figure, it turns out that < AOE = i (since L1 is parallel to L2, the corresponding angles are equal)
i = 2r, which implies that sin i/ sinr = μ, or 2cosr = μ, or r = 30° and i = 60°, which is the answer.
I do not understand why < ABO = r. Why is it so? It'd be helpful if I someone could come up with a different way of approaching the problem.