Albert1
- 1,221
- 0
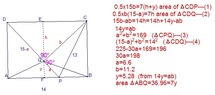
Rectangle $ABCD$ ,point $P$ on $\overline{AB}$ and point $Q$ on $\overline{DP}$ respectively
given: $\overline{AB}=14,\overline{CP}=13$. and $\overline{DP}=15$, if $\overline{CQ}\perp \overline{DP}$ on $Q$
please find the area of $\triangle ABQ$
given: $\overline{AB}=14,\overline{CP}=13$. and $\overline{DP}=15$, if $\overline{CQ}\perp \overline{DP}$ on $Q$
please find the area of $\triangle ABQ$