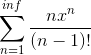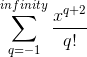The discussion focuses on finding an expression for the sum of a power series using Maclaurin series techniques, particularly the series for e^x. Participants suggest rewriting terms and splitting the series into two separate sums to simplify the process. The importance of handling specific terms, such as the n = 1 term, is emphasized to avoid incorrect cancellations that could lead to undefined expressions. An alternative approach using derivatives is also presented, which ultimately leads to the same result of x(1+x)e^x. The conversation highlights the necessity of careful manipulation of series and the potential pitfalls in handling factorial terms.