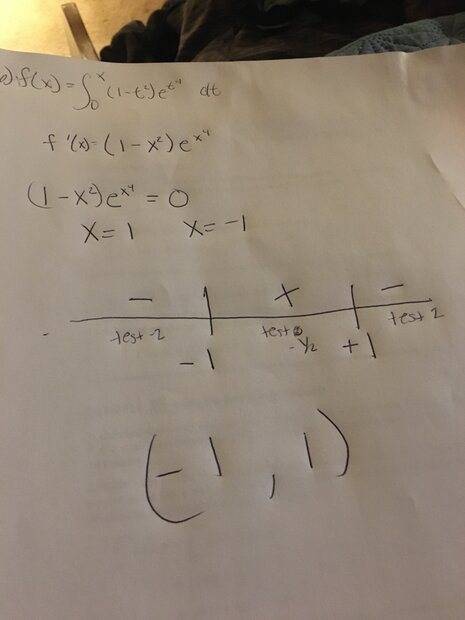Homework Help Overview
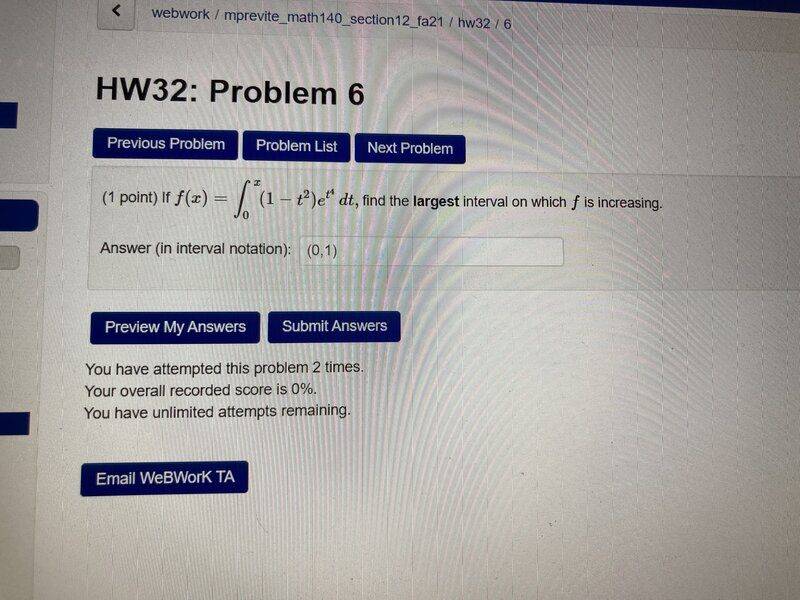
The discussion revolves around determining the largest interval on which a function is increasing, specifically focusing on the nuances between increasing and strictly increasing functions. The original poster presents a problem involving the derivative of a function defined by an integral.
Discussion Character
- Conceptual clarification, Assumption checking, Problem interpretation
Approaches and Questions Raised
- Participants explore the distinction between increasing and strictly increasing functions, questioning whether endpoints should be included in the interval. There are discussions about the implications of the derivative's sign and the effects of negative values on the integral.
Discussion Status
Participants are actively engaging with the problem, raising questions about the original poster's assumptions and the interpretation of the function's behavior. Some guidance has been offered regarding the nature of the derivative and its implications for the interval of increase.
Contextual Notes
There is uncertainty regarding the limits of integration and the domain of the function, which may affect the interpretation of the problem. The original poster's work is critiqued, and the potential for ambiguity in the problem setup is acknowledged.