MHB Find the number of distinct real roots

[anemone]

Let $f(x)=x^3-3x+1$. Find the number of distinct real roots of the equation $f(f(x))=0$.

 

[juantheron]

Just asking

I am getting Total no. of real solution is $ = 7$

Is is Right or not

Thanks

 

[mathbalarka]

Quite a nice bit of a problem you've got there. Here's my solution --

Spoiler

Finding the real roots of $$f(f(x)) = 0$$ is equivalent to finding the ones of $$f(x) = x_i$$ where $$x_i$$ for i = 1, 2, 3 are the (real) roots of f(x).

We see that the roots of $$f(x)$$ are all real as the discriminant is positive. An inspection of $$f(x) = x^3 - 3x + 1$$ can be considered at the intervals $$[-2, -1] \cup [-1, 0] \cup [0, 1] \cup [1, 2]$$ to find out that three roots lie precisely in between the first, third and the fourth interval.

Note that for the equation $$f(x) = x_i$$ to have all real root, the discriminant must be positive, implying the $$-2 \leq 1 - x_i \leq 2$$. The first root lies between [-2, -1], so $$1 - x_1$$ lies in between 2 and 3 and hence the discriminant comes down to a negative value, so one real root here exists and the other twos are complex conjugates of each other in $$\mathbb{C}$$.

For the second root, it lies between 0 and 1, so $$1 - x_2$$ lies in between 2 and -2 obviously enough. The same applies for the third root. So we have 3 real roots each for these two.

So, the total number of real roots are 1 + 3 + 3 = 7.

Balarka
.

 

[anemone]

Just asking

I am getting Total no. of real solution is $ = 7$

Is is Right or not

Thanks

Yes, 7 is the correct answer!:)

And thanks to you, Balarka, for participating and for your correct answer with your nice method!

 

[anemone]

Spoiler

Finding the real roots of $$f(f(x)) = 0$$ is equivalent to finding the ones of $$f(x) = x_i$$ where $$x_i$$ for i = 1, 2, 3 are the (real) roots of f(x).

.

Spoiler

Hey Balarka,

Spoiler

I really like it you mentioned that to solve for $x$ in $$f(f(x)) = 0$$ is equivalent to solve for $$f(x) = x_i$$ where $$x_i$$ for i = 1, 2, 3 are the (real) roots of f(x).

And if I may use this idea to solve for the problem, I found out the total number of real roots for $$f(f(x)) = 0$$ are 7 as well, and this method is so much better than my first approach and thank you, Balarka for showing me something that I don't know!

View attachment 1575
[TABLE="class: grid, width: 500"]
[TR]
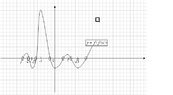
[TD]Solving for the number of real roots of $$f(x) = x_1=root_1$$ means the same thing as finding the number of intersection points between the curve $y=f(x)$ and $y=root_1$, as shown by the green line and we see that in this case we have only one real root for $$f(x) = x_1=root_1$$.[/TD]
[TD]Solving for the number of real roots of $$f(x) = x_2=root_2$$ means the same thing as finding the number of intersection points between the curve $y=f(x)$ and $y=root_2$, as shown by the purple line and we see that in this case we have only one real root for $$f(x) = x_2=root_2$$.[/TD]
[TD]Solving for the number of real roots of $$f(x) = x_3=root_3$$ means the same thing as finding the number of intersection points between the curve $y=f(x)$ and $y=root_3$, as shown by the orange line and we see that in this case we have only one real root for $$f(x) = x_3=root_3$$.[/TD]
[/TR]
[/TABLE]

So there are a total of 7 intersection points and hence there are 7 real roots for $$f(f(x)) = 0$$!

Thanks!

 

[mathbalarka]

this method is so much better than my first approach

May I see your approach on this problem?

Balarka
.

 

[anemone]

May I see your approach on this problem? Balarka .

Spoiler

My first approach revolves around checking the nature of the curve of the function of $f(f(x))$ from its first and second derivative expression. If we let $f(x)=x^3-3x+1$ and $g(x)=f(f(x))=(f(x))^3-3(f(x))+1$, we find

[TABLE="class: grid, width: 800"]
[TR]
[TD]$f(x)=x^3-3x+1$[/TD]
[TD]$g(x)=f(f(x))=(f(x))^3-3(f(x))+1$[/TD]
[/TR]
[TR]
[TD]$f'(x)=3x^2-3=3(x^2-1)=3(x+1)(x-1)$

$\rightarrow f'(x)=0$ iff $3(x+1)(x-1)=0$ or $x=\pm1$.[/TD]
[TD]$g'(x)=3f(x)^2f'(x)-3f'(x)=3f'(x)((f(x))^2-1)$

$\rightarrow g'(x)=0$ iff $x=\pm1$, $x=\pm \sqrt{3}$, or $x=-2$ or $x=0$.[/TD]
[/TR]
[TR]
[TD]$f''(x)=6x$[/TD]
[TD]$g''(x)=6f(x)(f'(x))^2+3f''(x)((f(x))^2-1)$[/TD]
[/TR]
[/TABLE]

I then made another table to determine the nature of the critical points as follows:
[TABLE="class: grid, width: 500"]
[TR]
[TD]$x$[/TD]
[TD]-2[/TD]
[TD]$-\sqrt{3}$[/TD]
[TD]-1[/TD]
[TD]0[/TD]
[TD]1[/TD]
[TD]$\sqrt{3}$[/TD]
[/TR]
[TR]
[TD]$f(x)$[/TD]
[TD]-1[/TD]
[TD]1[/TD]
[TD]3[/TD]
[TD]1[/TD]
[TD]-1[/TD]
[TD]1[/TD]
[/TR]
[TR]
[TD]$f'(x)$[/TD]
[TD]9[/TD]
[TD]6[/TD]
[TD]0[/TD]
[TD]-3[/TD]
[TD]0[/TD]
[TD]6[/TD]
[/TR]
[TR]
[TD]$f''(x)$[/TD]
[TD]-12[/TD]
[TD]$-6\sqrt{3}$[/TD]
[TD]-6[/TD]
[TD]0[/TD]
[TD]6[/TD]
[TD]$6\sqrt{3}$[/TD]
[/TR]
[TR]
[TD]$g(x)$[/TD]
[TD]3[/TD]
[TD]-1[/TD]
[TD]19[/TD]
[TD]-1[/TD]
[TD]3[/TD]
[TD]-1[/TD]
[/TR]
[TR]
[TD]$g'(x)$[/TD]
[TD]0[/TD]
[TD]0[/TD]
[TD]0[/TD]
[TD]0[/TD]
[TD]0[/TD]
[TD]0[/TD]
[/TR]
[TR]
[TD]$g''(x)$[/TD]
[TD]-486[/TD]
[TD]216[/TD]
[TD]-144[/TD]
[TD]54[/TD]
[TD]0[/TD]
[TD]216[/TD]
[/TR]
[/TABLE]

And plot a rough sketch to determine the number of real roots of the function of $f(f(x))=0$:

View attachment 1584

From the graph we can tell there are 7 real roots of the function of $f(f(x))=0$.

 

[mathbalarka]

Hmm... very nice. I like the way you analyzed the behavior of f(f(x)), very well done. Mine may have been a little time consuming but this one is more representative.

PS I particularly like this solution. (Mmm)

 

[anemone]

Hmm... very nice. I like the way you analyzed the behavior of f(f(x)), very well done. Mine may have been a little time consuming but this one is more representative.

PS I particularly like this solution. (Mmm)

Thank you for the compliment, Balarka!

And I must give full credit to Opalg, a very nice mentor here for giving me idea (from another question) to solve the problem!