youmei0426
- 18
- 0
- Homework Statement
- For the circuit below find:
the rms current drawn from the 240 V rms supply if the frequency is 50 Hz, and the phase of the current relative to the applied voltage.
- Relevant Equations
- Z(R) = R
Z(C) = -i/(wC)
Z(L) = iwL
where Z is complex impedance, R is resistance, w is angular frequency, L is inductance and C is capacitance
My first idea was to find the total impedance of the circuit, but I think viewing the two parallel resistors as one resistor of 0.5 Ohm isn't the correct way? I don't know how to simply this series / parallel circuit further to find Z total.
Then I tried to use Kirchhoff's law to the loop on the left, and got the equation 240 - I1R - (I1-I2)R = 0. Since R = `1, the equation was simplified into
I2 - 2I1 + 240 = 0.
Doing the same thing for the loop on the right, and getting the voltages by using IZ, I had the equation
-I2*(-i/(wC)) - I2*iwL - I2 + (I1 - I2)=0
Making the real part of the above equation to zero and solving for the two equations, I got I1 = 160A and I2 = 80A. However, the answer is supposed to be 126 A with a phase difference of 6.4 degree.
Am I approaching the question in the wrong way?? Thanks in advance for your help!
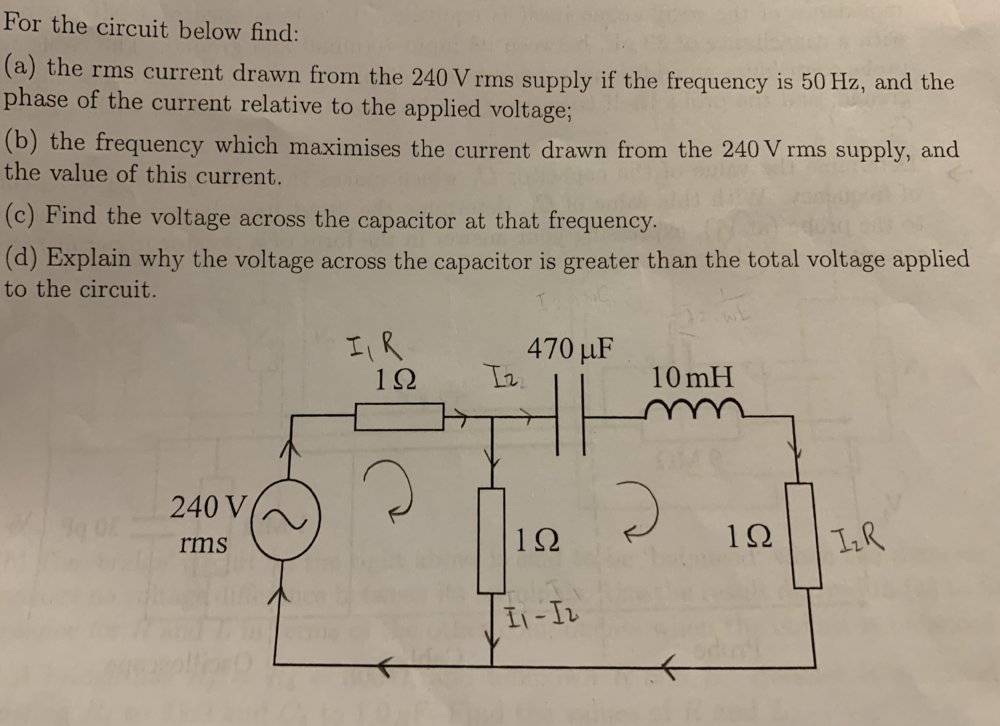
Then I tried to use Kirchhoff's law to the loop on the left, and got the equation 240 - I1R - (I1-I2)R = 0. Since R = `1, the equation was simplified into
I2 - 2I1 + 240 = 0.
Doing the same thing for the loop on the right, and getting the voltages by using IZ, I had the equation
-I2*(-i/(wC)) - I2*iwL - I2 + (I1 - I2)=0
Making the real part of the above equation to zero and solving for the two equations, I got I1 = 160A and I2 = 80A. However, the answer is supposed to be 126 A with a phase difference of 6.4 degree.
Am I approaching the question in the wrong way?? Thanks in advance for your help!