Wm_Davies
- 51
- 0
1. Homework Statement [/b]
I need help with part (a) of this problem. (See attachment)
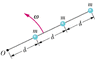
In Fig. 11-45, three particles of mass m = 3.9 kg are fastened to three rods of length d = 0.40 m and negligible mass. The rigid assembly rotates about point O at angular speed ω = 9.1 rad/s. About O, what are (a) the rotational inertia of the assembly, (b) the magnitude of the angular momentum of the middle particle, and (c) the magnitude of the angular momentum of the assembly?
Rotational Inertia for a rod = \frac{1}{12}(ML^{2})
Rotational Inertia for a Particle = mr^2 (Where r is the distance from the point of rotation)
First I took the three rods and made them into one long one with three particles attached to it and used the parallel axis theorem to adjust the rotational inertia for the rod.
Which gave me the equation of...
\frac{1}{12}[ML^{2}+ML^{2}]+m[(r)^{2}+(2r)^{2}+(3r)^{2}]=I
I substitute in the notation used in the problem and remove the M for the rod since it is negligible.
\frac{1}{12}[(3d)^{2}+(1.5d)^{2}]+m[(d)^{2}+(2d)^{2}+(3d)^{2}]=I
After plugging in the numbers for this I had gotten...
\frac{1}{12}[(3*.3)^{2}+(1.5*.3)^{2}]+4.2[(.3)^{2}+(2*.3)^{2}+(3*.3)^{2}]=I
Which gave me the result of...
5.37638 kg*m^2
Which is not correct, but I cannot see what I did wrong. I would appreciate any help. I know that the correct answer is 5.292 kg*m^2
I need help with part (a) of this problem. (See attachment)
In Fig. 11-45, three particles of mass m = 3.9 kg are fastened to three rods of length d = 0.40 m and negligible mass. The rigid assembly rotates about point O at angular speed ω = 9.1 rad/s. About O, what are (a) the rotational inertia of the assembly, (b) the magnitude of the angular momentum of the middle particle, and (c) the magnitude of the angular momentum of the assembly?
Homework Equations
Rotational Inertia for a rod = \frac{1}{12}(ML^{2})
Rotational Inertia for a Particle = mr^2 (Where r is the distance from the point of rotation)
The Attempt at a Solution
First I took the three rods and made them into one long one with three particles attached to it and used the parallel axis theorem to adjust the rotational inertia for the rod.
Which gave me the equation of...
\frac{1}{12}[ML^{2}+ML^{2}]+m[(r)^{2}+(2r)^{2}+(3r)^{2}]=I
I substitute in the notation used in the problem and remove the M for the rod since it is negligible.
\frac{1}{12}[(3d)^{2}+(1.5d)^{2}]+m[(d)^{2}+(2d)^{2}+(3d)^{2}]=I
After plugging in the numbers for this I had gotten...
\frac{1}{12}[(3*.3)^{2}+(1.5*.3)^{2}]+4.2[(.3)^{2}+(2*.3)^{2}+(3*.3)^{2}]=I
Which gave me the result of...
5.37638 kg*m^2
Which is not correct, but I cannot see what I did wrong. I would appreciate any help. I know that the correct answer is 5.292 kg*m^2
Attachments
Last edited: