Find x-Bar Location for Distributed Loading | Torque Calculation

[shreddinglicks]

Homework Statement

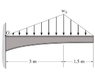
Replace the distributed loading with an equivalent resultant
force, and specify its location on the beam measured from
point O.

W = 3 kn/m

Homework Equations

F*xbar = torque

The Attempt at a Solution

I got the resultant forces:

(1/2)*3*3 = 4.5 kn
(1/2)*1.5*3 = 2.25 kn

4.5 + 2.25 = 6.75 kn

I know my general equation is:

6.75*xbar = torque

I want to solve for xbar.

xbar should equal 2.5m

 

[SteamKing]

What's the centroidal location of a right triangle? Your distributed load can be broken up into two triangular loads.

 

[shreddinglicks]

What's the centroidal location of a right triangle? Your distributed load can be broken up into two triangular loads.

I'm unsure, could you explain it to me?

 

[SteamKing]

If the centroid of a rectangle is located at half the length or half the depth, what is the centroid of a triangle?

If you're still stumped, you can always google 'centroid of right triangle'

 

[shreddinglicks]

If the centroid of a rectangle is located at half the length or half the depth, what is the centroid of a triangle?

If you're still stumped, you can always google 'centroid of right triangle'

If I multiply both distances by 1/3, I still do not get the proper answer.

 

[shreddinglicks]

I see, so when I approach the triangle from the one side I have 1/3 so the rest must be 2/3. But how do I know which is the 1/3 side and which is the 2/3 side?

 

[SteamKing]

I see, so when I approach the triangle from the one side I have 1/3 so the rest must be 2/3. But how do I know which is the 1/3 side and which is the 2/3 side?

If you have a right triangle with the pointy end at O, how far from O will the centroid be, 1/3 of the length of the base or 2/3 of the length of the base?
Remember, the location of the centroid coincides with the balance point of the triangle.

 

[shreddinglicks]

If you have a right triangle with the pointy end at O, how far from O will the centroid be, 1/3 of the length of the base or 2/3 of the length of the base?
Remember, the location of the centroid coincides with the balance point of the triangle.

It would have to be 2/3.

So, if I had a problem where I had to find, say a location at point, "A" that was directly under W. The distance would then be 1/3 for each triangle?

 

[SteamKing]

It would have to be 2/3.

So, if I had a problem where I had to find, say a location at point, "A" that was directly under W. The distance would then be 1/3 for each triangle?

I'm not sure what you are asking here. The choice of whether to use 1/3 or 2/3 of the length of the base as the centroid depends on the orientation of the triangle.

 

[shreddinglicks]

I'm not sure what you are asking here. The choice of whether to use 1/3 or 2/3 of the length of the base as the centroid depends on the orientation of the triangle.

I meant a situation like the one pictured. I would use 1/3 for each triangle, and I would use 1/2 for the rectangle, correct?

 

[SteamKing]

I meant a situation like the one pictured. I would use 1/3 for each triangle, and I would use 1/2 for the rectangle, correct?

1/3 of the base for each triangle would be OK, as long as the reference was taken about a vertical line running thru the support at B.

 

[shreddinglicks]

I see, thanks for your help!