Finding angular speed geometrically

[PhysHobbiest]

Homework Statement

As the title says, I was simply looking to geometrically find the angular speed of an object traveling along a line on the x axis with respect to a position at a height h on the z axis.

Relevant Equations

tan(θ) = x/h

So clearly the easiest way to relate the angular speed to the linear speed would be to start from $\tan(θ) = x/h$ and take a time derivative of both sides. However, it also shouldn't be difficult to find the angular speed geometrically. Using the diagram below one can see that:

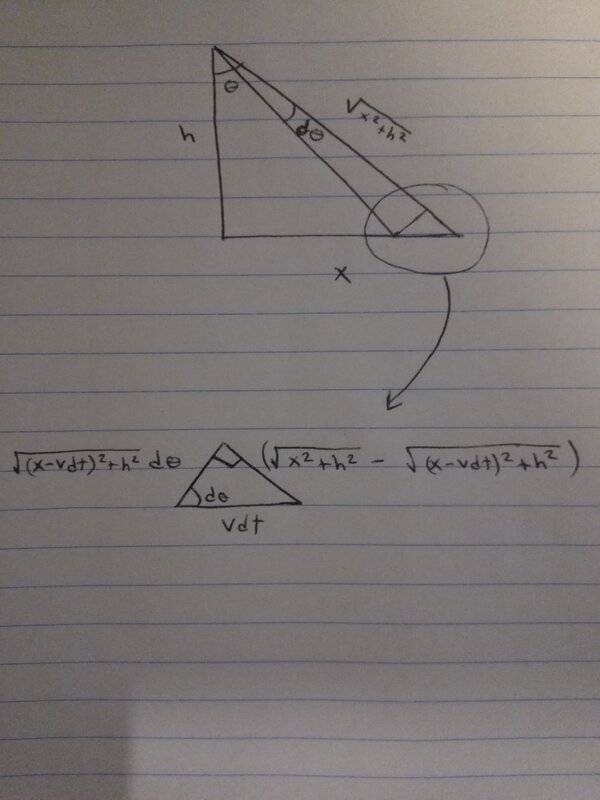
$sin(dθ) = \frac {{\sqrt {x^2+h^2}}-{\sqrt {(x-vdt)^2+h^2}}} {vdt}$

which is approximately (after a small angle approx and using the definition of the derivative)

$dθ = \frac {d} {dx} \sqrt {x^2+h^2}$

which yields

$dθ = \frac {x} {\sqrt {x^2+h^2}}$

Now this I believe is nonsense, and I'm having difficulty figuring out exactly what went wrong. Did I mess up along the way, or were the approximations I made not good ones? My guess is any approximation that would leave an infinitesimal value on only one side of the equation is a bad one. Just looking for confirmation here.

 

[anuttarasammyak]

Please check your result with my calculation.
$$x=h\tan\theta$$
$$\frac{dx}{dt}=h \sec^2\theta \frac{d\theta}{dt}=\frac{h^3}{h^2+x^2}\frac{d\theta}{dt}$$

EDIT calculation error as pointed out in #3. Thanks.

 

[PhysHobbiest]

Please check your result with my calculation.
$$x=h\tan\theta$$
$$\frac{dx}{dt}=h \sec^2\theta \frac{d\theta}{dt}=\frac{h^3}{h^2+x^2}\frac{d\theta}{dt}$$

Thanks for the input, I believe you accidentally inverted $\sec^2\theta$ when you expanded it out. The answer should look like

$\frac {dx} {dt} = \frac {h^2 + x^2} {h} \frac {d\theta}{dt}$

I'm aware of what the answer should be, I was simply looking for the flaw in my above reasoning. It was unsettling to me that the simple geometric reasoning I was using was yielding the nonsense that I got.

 

[anuttarasammyak]

The first formula in post #1
$$\sin(d\theta)=...$$
should be
$$\sin\theta =...$$ ?
If so it tells just obvious
$$sin \theta = \frac{x}{\sqrt{x^2+h^2}}$$

 

[PhysHobbiest]

oof, thanks for being another set of eyes on that. I don't know how I mistaked θ with dθ there.