Finding average force with out taking mass into account

[xrotaryguy]

If a .045kg ball takes off at 41m/s after being hit,

a.) How much work is done on the ball?

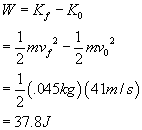
b.) Assume that the force of the club acts parallel to the motion of the ball, and that the club is in contact with the ball for .010m. Ignore the mass of the ball and find the average force applied to the ball.

I don't know how to do this. I want to take the mass of the ball into account with the F=mv formula. What do I do?

 

[Hootenanny]

I think the question wants you to make use of the fact that the work done by a constant force is the product of that force and the distance moved in the direction of that force.

 

[xrotaryguy]

Excellent! That was exactly what I needed. Thanks!