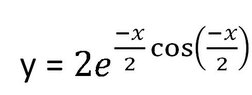You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
MHB Finding Derivative of a Function
- Thread starter rcs1
- Start date
-
- Tags
- Derivative Function
Physics news on Phys.org
Mathwebster
- 185
- 0
If $y = e^{f(x)}$ then $y' = e^{f(x)} f'(x) $. Try that.
Prove It
Gold Member
MHB
- 1,434
- 20
rcs said:I am so happy that i found this site because it's been few days now that i haven't solved this function.
I hope somebody here can help me on finding the derivative of this function..Thank you so much.
What Danny is using is the Chain Rule. The more general result of the chain rule is that if $ \displaystyle y = y \left( u(x) \right) $ (a function of a function), then $ \displaystyle \frac{dy}{dx} = \frac{du}{dx} \cdot \frac{dy}{du} $.
So in your case, you have $ \displaystyle y = 2e^{-\frac{x}{2}\cos{\left( -\frac{x}{2} \right)}} $, so let $ \displaystyle u = -\frac{x}{2}\cos{\left( - \frac{x}{2} \right)} $ so that $ \displaystyle y = 2e^u $. Can you now evaluate $ \displaystyle \frac{du}{dx} $ and $ \displaystyle \frac{dy}{du} $?
rcs1
- 10
- 0
sir,
do u mean that i have to get the derivative first of the whatever is y = 2e^u
does that ln y = ln e^2u?
then ln y = 2u remain and manipulate for the derivate of 2u?
hope u i am doing it correctlyThank you
do u mean that i have to get the derivative first of the whatever is y = 2e^u
does that ln y = ln e^2u?
then ln y = 2u remain and manipulate for the derivate of 2u?
hope u i am doing it correctlyThank you
Prove It
Gold Member
MHB
- 1,434
- 20
rcs said:sir,
do u mean that i have to get the derivative first of the whatever is y = 2e^u
does that ln y = ln e^2u?
then ln y = 2u remain and manipulate for the derivate of 2u?
hope u i am doing it correctlyThank you
No, that's incorrect. Say we had $ \displaystyle y = 2e^x $, what would $ \displaystyle \frac{dy}{dx} $ be?
To find $ \displaystyle \frac{dy}{du} $ from $ \displaystyle y = 2e^u $ is identical, it's just that the function is a function of u instead of x, and the derivative is taken with respect to u instead of x.
rcs1
- 10
- 0
:( made me so confuseProve It said:No, that's incorrect. Say we had $ \displaystyle y = 2e^x $, what would $ \displaystyle \frac{dy}{dx} $ be?
To find $ \displaystyle \frac{dy}{du} $ from $ \displaystyle y = 2e^u $ is identical, it's just that the function is a function of u instead of x, and the derivative is taken with respect to u instead of x.
Prove It
Gold Member
MHB
- 1,434
- 20
rcs said::( made me so confuse
What's the derivative of $ \displaystyle e^x $?
rcs1
- 10
- 0
isn't not e^x also?Prove It said:What's the derivative of $ \displaystyle e^x $?
Jameson
- 4,533
- 13
Correct! Now consider the case of $ \displaystyle e^{f(x)}$. The derivative is $ \displaystyle e^{f(x)}*f'(x)$. What is f(x) in this problem and what is the derivative of f(x)?
[sp]$ \displaystyle f(x)= -\frac{x}{2}\cos{\left( - \frac{x}{2} \right)} $[/sp]
[sp]$ \displaystyle f(x)= -\frac{x}{2}\cos{\left( - \frac{x}{2} \right)} $[/sp]
Last edited:
rcs1
- 10
- 0
that is my problem now... i have a hard of solving trigonometry :( so hard for me on that ...Jameson said:Correct! Now consider the case of $ \displaystyle e^{f(x)}$. The derivative is $ \displaystyle e^{f(x)}*f'(x)$. What is f(x) in this problem and what is the derivative of f(x)?
[sp]$ \displaystyle f(x)= -\frac{x}{2}\cos{\left( - \frac{x}{2} \right)} $[/sp]
rcs1
- 10
- 0
can anybody show or help me on a step by step on this please?
thanks a lot
thanks a lot
earboth
- 67
- 0
rcs said:can anybody show or help me on a step by step on this please?
thanks a lot
One personal remark first: I don't like the idea that we should do your work ...
1. You must see at once that
$ f(x)=2 e^{-{\tfrac12}x \cdot \cos\left(-{\tfrac12}x \right)} $ is an exponential function.
What function do you get if you differentiate $ f(x)=e^x $ ?
2. You must see at once that your function is not a simple exponential function. The exponent is a function itself. Thus you have to use the chain rule when differentiating your function:
$ f(x) = e^{u(x)}~\implies~ f'(x) = e^{u(x)} \cdot u'(x) $
3. You must see at once that the exponent of your function is a product of functions. To differentiate a product of functions you have to use the product rule:
$ f(x) = g(x) \cdot h(x) ~ \implies~ f'(x) = h(x) \cdot g'(x) + g(x) \cdot h'(x) $
With your function you have:
$ g(x) = -{\frac12}x $ and
$ h(x) = \cos\left( -\frac12 x \right) $
4. You are supposed to know that
$ \sin'(x) = \cos(x) $ ...$ \cos'(x) = -\sin(x) $ ... $ -\sin'(x) = -\cos(x) $ ...$ -\cos'(x) = \sin(x) $ ...
That means during the differentiation of the exponent you have to differentiate the cos-function. BUT: the argument of the cos-function isn't a simple x therefore you must use the chain rule here:
$ f(x) = \cos(u(x))~\implies~f'(x) = -\sin(u(x)) \cdot u'(x) $
5. Now collect all the results to one brand-new function.
rcs1
- 10
- 0
Thank you so much... i only thought of the use of term help in this website... this is the significance of this website now... because there are some instances that some people really don't know that problem and seek for help...earboth said:One personal remark first: I don't like the idea that we should do your work ...
1. You must see at once that
$ f(x)=2 e^{-{\tfrac12}x \cdot \cos\left(-{\tfrac12}x \right)} $ is an exponential function.
What function do you get if you differentiate $ f(x)=e^x $ ?
2. You must see at once that your function is not a simple exponential function. The exponent is a function itself. Thus you have to use the chain rule when differentiating your function:
$ f(x) = e^{u(x)}~\implies~ f'(x) = e^{u(x)} \cdot u'(x) $
3. You must see at once that the exponent of your function is a product of functions. To differentiate a product of functions you have to use the product rule:
$ f(x) = g(x) \cdot h(x) ~ \implies~ f'(x) = h(x) \cdot g'(x) + g(x) \cdot h'(x) $
With your function you have:
$ g(x) = -{\frac12}x $ and
$ h(x) = \cos\left( -\frac12 x \right) $
4. You are supposed to know that
$ \sin'(x) = \cos(x) $ ...$ \cos'(x) = -\sin(x) $ ... $ -\sin'(x) = -\cos(x) $ ...$ -\cos'(x) = \sin(x) $ ...
That means during the differentiation of the exponent you have to differentiate the cos-function. BUT: the argument of the cos-function isn't a simple x therefore you must use the chain rule here:
$ f(x) = \cos(u(x))~\implies~f'(x) = -\sin(u(x)) \cdot u'(x) $
5. Now collect all the results to one brand-new function.
thanks so much!
sweer6
- 10
- 0
if y = e^(f(x) then dy/dx = f'(x)*e^(f(x))
this means to multiply the original function (e^x) by the deravative of x which is positive 1 (+1), to give itself as the differential. The differential of e^x = e^x. (this is pretty cool)
or y = e^x then dy/dx = e^x.
this means to multiply the original function (e^x) by the deravative of x which is positive 1 (+1), to give itself as the differential. The differential of e^x = e^x. (this is pretty cool)
or y = e^x then dy/dx = e^x.
Similar threads
- Replies
- 5
- Views
- 3K
- Replies
- 15
- Views
- 2K
- Replies
- 15
- Views
- 2K
- Replies
- 12
- Views
- 3K
- Replies
- 8
- Views
- 2K
- Replies
- 16
- Views
- 2K
- Replies
- 3
- Views
- 4K
- Replies
- 17
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 53
- Views
- 5K
Hot Threads
-
I Harmonic series Ʃ1/n diverges but p-series Ʃ(1/n)^p diverges?
- Started by Dimwitted_UniStudent
- Replies: 4
- Calculus
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math