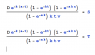I Finding number of solutions for a system of equations?

[kochibacha]

Is there any general theorem on finding number of solutions to this system of equations(D e^(-k (a - t)) (1 - e^-kt) (1 - e^(-a k n)))/((1 - e^(-a k)) k t v) = S

(G e^(-k (a - t)) (1 - e^-kt) (1 - e^(-a k n)))/((1 - e^(-a k)) k t v) = Twhere k,v are variables and others are constant

*edited equations

 

[mfb]

The two equations look identical. If S=T that is fine, just a bit redundant. It is easy to solve for v(k) then, which has a unique solution everywhere apart from k=0 where the equation cannot be satisfied.

 

[kochibacha]

The two equations look identical. If S=T that is fine, just a bit redundant. It is easy to solve for v(k) then, which has a unique solution everywhere apart from k=0 where the equation cannot be satisfied.

thanks for the fast reply. The problem was actually Mathematica cannot solve these system of equations (picture attached) so I used Excel Solver to find k,v satisfying those two equations. I just wonder that the k,v that I got are the only real number solutions to this system.

 

[mfb]

There is no solution. Your equations are "250 * something = 50 && 375 * something = 80", which quickly leads to a contradiction.