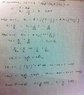MissP.25_5
- 329
- 0
Hello again. I hope someone could check if I got the answers correct.
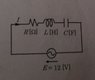
The magnitude of the current I in resonant state was 3[A]. When the angular frequency of the power supply was 1 [rad/s] and 2[rad/s], the magnitude of current I became 1/√2 of the value when resonance occurred. Find R, L, C.
The magnitude of the current I in resonant state was 3[A]. When the angular frequency of the power supply was 1 [rad/s] and 2[rad/s], the magnitude of current I became 1/√2 of the value when resonance occurred. Find R, L, C.