Coder74
- 20
- 0
Hello,
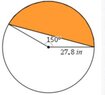
I've done something similar to this before but this question is really different because it contains two shapes. Now I'm really confused and I really appreciate the help~! View attachment 6004
-Cheers
I've done something similar to this before but this question is really different because it contains two shapes. Now I'm really confused and I really appreciate the help~! View attachment 6004
-Cheers