Finding the Area of an Elliptical Region Using Integration

[Illusionist]

Homework Statement

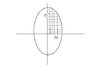
Find the area of the region bounded by the positive x-axis,
the positive y-axis and the curve:
(x^2) +[(y^2)/4] = 1
using vertical and horizontal strips.

Homework Equations

Basically I just tried to use integration to find the area, but I suspect I have made a mistake about what the interval for the integration should be.

The Attempt at a Solution

Vertical Strips -
Transposing the equation gives me: y=Sqrt[1-(x^2)]
So basically I know that the area would be the integral of this but not 100% sure between what intervals. I suspect, from a graph obtained from a graphics calculator, that is between 1 and -1.
Hence area= Integral of Sqrt[1-(x^2)] between 1 and -1.
The integral I got to be Sqrt[1-(x^2)]x + arcsin(x), from a online integration calculator. Between 1 and -1 this would give a area of Pi.

Horizontal Strips -
Transposing the equation gives me: x=Sqrt[1-[(y^2)/4])
Now the integral of this I got to be [(1/4)Sqrt(4-(y^2))].y + arcsin(y/2)
From the same graph I assume the interval for this one should be from 2 to 0. But substituting these values gives me a area of (Pi/2).

Obviously the areas need to be the same and they aren't! I'm positive that it is the intervals for integration that I am having trouble with, but where the mistake is and why I am not sure. My only guess is that becaise it says positive x and y-axis that the interval for the vertical strips should be 1 to 0, but not sure and would this approach change anything I did for the horizontal? Any help or advice would be great. Thanks guys!

 

[matness]

here is the mistake

y=Sqrt[1-(x^2)]

you forgot 4
y=4*Sqrt[1-(x^2)]
and interval is from 0 to 1
can you see why?

 

[matness]

and just a recommendation: It is better to get use to find integrals by hand rather than calculator;)

 

[Illusionist]

here is the mistake

you forgot 4
y=4*Sqrt[1-(x^2)]
and interval is from 0 to 1
can you see why?

Yeah sorry. Between 0 to 1 would make sense, as both horizontal and vertical would give me an area of (Pi/2) now, but using the same sort of approach is my horizontal method still right?
Thanks for that matness, and yeah I really should stop relying so heavily on my calculator.

 

[matness]

Sorry i did a mistake also :
y=2*sqrt(1-x^2)

 

[matness]

you can trust calculators but i want to say it is better doing by hand in order to learn and useful for other calculations
p.s.: Stop relying heavily what other people say:)

 

[Illusionist]

Yeah I get what you mean matness, thanks for everything mate. I just not really confident with what I do and why, like in this question. Still not sure what I did was right for the horizontal strips.

 

[matness]

The equation says the curve is an ellipse.(see the image below)
if x = 0 then y = 2 or-2 so graph intersect the y-ax's at 2 and =2
if y=0 then x=1 or -1 similarly this means the graph intersects x-axis at this points
Anyway if you understood the graph no problem ? it is 1&4 of an ellipse

first of all integral means infinitesimall sum. Roughly you can either sum up the areas of horizontal strips or vertical strips .
lets look at the horizontal sum case
one side of the rectangle is dy and the other side is x which is equal to Sqrt[1-[(y^2)/4]
and you have a sum from 0 to 2 because your region is given in this way

the region bounded by the positive x-axis,
the positive y-axis and the curve:
(x^2) +[(y^2)/4] = 1

so you have
area=integral from 0 to 2 of Sqrt[1-[(y^2)/4]dy
vertical strips case is similliar

you can check your result by using area formula for ellipses.you have to find 1/4 of the area of the ellipse

p.s.what i wrote is not so formal things i just try to explain intuitively
i hope this does not make you confuse