Finding the maximum acceleration

[Saitama]

Homework Statement

Homework Equations

The Attempt at a Solution

I don't know how to make the equations here.

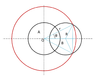
When the balls are penetrating each other, a cavity is being formed due to overlap of the negative and positive charges. The size of this cavity keeps on increasing. The trouble is I cannot figure out the instant of maximum velocity and the equations to write down. I need a few hints to begin with.

Any help is appreciated. Thanks!

 

[voko]

The attachment is not shown. It is said to be invalid.

 

[Saitama]

The attachment is not shown. It is said to be invalid.

Does it work now?

 

[voko]

If a function reaches a maximum, what happens to its derivative? What does that mean in this case?

 

[Saitama]

If a function reaches a maximum, what happens to its derivative? What does that mean in this case?

The derivative is zero but to find the maximum, I need the function. Can you please give me a few hints about finding the function? :)

 

[voko]

What is the derivative of velocity? What does that mean, physically, its being zero? When/where can that happen in this situation?

 

[Saitama]

What is the derivative of velocity?

Acceleration.

What does that mean, physically, its being zero?

It means acceleration is zero, the body is at rest or is moving with a constant velocity.

When/where can that happen in this situation?

I am not sure so I make a guess. It can happen when both the balls completely overlap. I think when the balls completely overlap, the net charge is zero so no electric force is acting, right?

 

[voko]

I agree with that. That gives you some important knowledge: you know at what separation between the centers their speed was 10 m/s. Can you proceed further?

 

[Saitama]

I agree with that. That gives you some important knowledge: you know at what separation between the centers their speed was 10 m/s. Can you proceed further?

The velocity is maximum when the separation is zero, right?

I can't think of anything about the next step. :(

 

[voko]

What is the potential energy of the system when the separation is zero?

 

[Saitama]

What is the potential energy of the system when the separation is zero?

Umm...zero?

 

[voko]

Why do you think it is zero?

 

[Saitama]

Why do you think it is zero?

There is no charge when separation is zero which led me to think that it is zero. Am I wrong?

 

[voko]

No charge means the force is zero, but that does not mean the potential energy is zero. We typically define potential energy in such a way that it is zero at the infinite separation. If it is defined like that, then your suggestion that the potential energy is zero at the zero separation is problematic with respect to conservation of energy. Can you see that?

 

[Saitama]

No charge means the force is zero, but that does not mean the potential energy is zero. We typically define potential energy in such a way that it is zero at the infinite separation. If it is defined like that, then your suggestion that the potential energy is zero at the zero separation is problematic with respect to conservation of energy. Can you see that?

I am not sure so I thought of starting with the definitions.

$$U(R)-U(0)=-\int_0^R \frac{kQq}{r^2}dr$$
(where both Q and q are positive)

$$U(R)-U(0)=\lim_{r\rightarrow 0}\frac{kQq}{r}-\frac{kQq}{R}$$

I don't see how defining U(0)=0 leads to complications. :(

 

[voko]

I am not sure so I thought of starting with the definitions.

$$U(R)-U(0)=-\int_0^R \frac{kQq}{r^2}dr$$
(where both Q and q are positive)

I am not sure what that equation means. What is $R$? Is it the size of the sphere? Then I do not see where you factor in the separation. If it is the separation, then I do not see how you account for separations less than the diameter of the spheres.

I don't see how defining U(0)=0 leads to complications. :(

Well, if it is zero both at the infinity and at the zero separation, then the kinetic energy must also be zero at the zero separation if it was zero at the infinity. Which, I think, quite obviously is an impossible result.

 

[Saitama]

I am not sure what that equation means. What is $R$? Is it the size of the sphere? Then I do not see where you factor in the separation. If it is the separation, then I do not see how you account for separations less than the diameter of the spheres.

Sorry, I should have been clear, I was taking a general case when a point charge q is taken from r=0 to r=R from a fixed point charge Q.

Well, if it is zero both at the infinity and at the zero separation, then the kinetic energy must also be zero at the zero separation if it was zero at the infinity. Which, I think, quite obviously is an impossible result.

I think I understand your point but I am still clueless about the given problem.

 

[voko]

Here is a question: what does the graph of the potential energy vs the separation look like?

 

[Saitama]

Here is a question: what does the graph of the potential energy vs the separation look like?

When the separation between the centre of balls is 2R, the potential energy is $-kQ^2/(2R)$. For separation greater than 2R, the graph increases and tends to zero at infinity. For separation less than 2R, I am not sure how the graph would look like as they begin to penetrate each other. Would the potential energy still be $-kQ^2/r$ where r is the separation between the centre of balls and r<2R?

 

[voko]

Remember that you have already established that the kinetic energy has a maximum at the zero separation. What about the potential energy?

 

[Saitama]

Remember that you have already established that the kinetic energy has a maximum at the zero separation. What about the potential energy?

If potential energy is still given $-kQ^2/r$, then at zero separation, it shoots to $-\infty$.

But initially, the energy of system is zero, so kinetic energy at zero separation must be equal to the potential energy.

 

[voko]

What is important is that the potential energy is some constant minus the potential energy. So when one is at a maximum, the other is at a minimum. Hence, the potential energy must be at a minimum at the zero separation. It can be also seen from the fact that at the zero separation the force is zero, and the force is the derivative of the potential energy.

Yet another way would be by saying "it is obvious that a stable equilibrium configuration of two equal shape, equal mass, opposite charge clouds is when they coincide completely".

So, what does the total graph look like? Where is it convex, where is it concave? Where is the inflection point? What is its significance?

 

[Saitama]

So, what does the total graph look like? Where is it convex, where is it concave? Where is the inflection point? What is its significance?

I don't understand why you ask me about the graph when it is simply a -1/r relationship.

http://www.wolframalpha.com/input/?i=y=-1/x

 

[voko]

The shape in the lower-right quadrant is correct only when the separation is greater than the diameter. At smaller separations, the graph is different. Which is obvious from the fact that at the zero separation it has a minimum, not a singularity.

 

[Saitama]

The shape in the lower-right quadrant is correct only when the separation is greater than the diameter. At smaller separations, the graph is different. Which is obvious from the fact that at the zero separation it has a minimum, not a singularity.

How do I find the expression for potential energy when the balls penetrate each other?

 

[voko]

I thought it would be useful for you to understand what the potential energy curve looks like before you go into finding the function.

The potential energy is the integral of the potential of one ball times the charge density of the other ball, taken over the volume of the other ball.

 

[Saitama]

The potential energy is the integral of the potential of one ball times the charge density of the other ball, taken over the volume of the other ball.

I am very sorry but I am honestly lost. I can't see how to set up the integral. I can find the volumes of non-overlapped and overlapped spaces using the spherical cap formulas (as rcgldr has indicated) but I don't know how to write down the integral.

According to your post,
$$U=\int \rho V d\tau $$

I can find $\rho$ but what do I substitute for V, the potential of one ball?

 

[rcgldr]

I am very sorry but I am honestly lost. I can't see how to set up the integral. I can find the volumes of non-overlapped and overlapped spaces using the spherical cap formulas (as rcgldr has indicated) but I don't know how to write down the integral.

I deleted that post, because I'm not sure that the net attractive force of the overlapped volume between the two spheres is zero, and I was going to repost after thinking about this further. I'm also stuck at what seems to be doing the equivalent of deriving Guass's law via calculus to handle the overlapped spheres.

As for the simpler approach, if the force between overlapped spheres is a linear function of d (d = distance between centers) (I'm not sure that it is linear though), then the force at d = 0 (force = zero) and the force at d = 2r (force = k q^2/((2 r)^2) are known values and an equation could be created for the force (force = d k q^2/((2 r)^3) . This could then be used to create an equation for the potential energy.

 

[voko]

I can find $\rho$ but what do I substitute for V, the potential of one ball?

Let's say one sphere is A, another is B. What is the potential of A at distance $z$ from its center if $z \ge R$? If $z < R$?

Now, let the centers of A and B be separated by $d$. Let $(x, y)$ be the coordinates of a point of B. What is its distance from the center of A? What is the potential of A at that point?

 

[voko]

In #29, I did not specify what $(x, y)$ was with respect to. Take care of that.

 

[voko]

Oops, I made another slip. We are dealing with 3D, so the point is $(x, y, z)$, but I used $z$ to mean something else.

Pranav, you will have to fix my mistakes and introduce some consistent notation.

 

[Saitama]

Let's say one sphere is A, another is B. What is the potential of A at distance $z$ from its center if $z \ge R$? If $z < R$?

For $z\geq R$, it is simply $kQ/z^2$.

For $z<R$, the potential is $\displaystyle \frac{kQ}{2R}\left(3-\frac{r^2}{R^2}\right)$

Now, let the centers of A and B be separated by $d$. Let $(x, y)$ be the coordinates of a point of B. What is its distance from the center of A? What is the potential of A at that point?

I take the sphere A to be centred at origin. The distance of $(x,y)$ from origin is $\sqrt{x^2+y^2}$. Potential at $(x,y)$ is calculated using the above formulas.

I was thinking that won't it be better to ask distance of $(x,y,z)$ from centre of A? We have a 3-dimensional ball, sorry if I am acting dumb.

EDIT: Okay, I see, we both posted at the same time. :)

So the distance from centre of A is $\sqrt{x^2+y^2+z^2}$.

 

[voko]

I would rather make the center of B the origin. I would further stack A on top (i.e., z-axis) of B and use spherical coordinates. Caveat: these suggestions are based solely on my gut feeling, so could be misleading.

Obviously, you will need to find a way to split the integration domain into two parts.

 

[Saitama]

I would rather make the center of B the origin. I would further stack A on top (i.e., z-axis) of B and use spherical coordinates. Caveat: these suggestions are based solely on my gut feeling, so could be misleading.

Obviously, you will need to find a way to split the integration domain into two parts.

I am not comfortable with spherical coordinates. I was trying something before you asked me to calculate the distance of $(x,y,z)$ from centre of A. Please look at the attachment. If my approach is too complicated, I would happily switch to spherical coordinates.

I consider a red sphere of radius r and thickness dr passing through the sphere B. This red sphere forms a spherical cap inside B. The area of the spherical cap is given $2\pi r^2(1-\cos\theta)$. I used the law of cosines and substituted $\cos\theta=\frac{r^2+d^2-R^2}{2rd}$. After some simplification, I get:

$$dA=\frac{\pi r}{d}\left(R^2-(r+d)^2\right)$$

Hence, the differential volume is $dV=(dA)dr$. Since I have the volume charge density, I can find the charge contained in it.

I would like to know if I am correct so far. :)

EDIT: I am not sure but I think dV should (dA)(rdθ) instead of (dA)dr.

 

[voko]

That looks correct to me, except that it should be $(r - d)^2$. And that should be just $A$, not $dA$, because the area is not a differential.