Kyp
- 2
- 0
Homework Statement
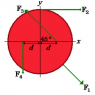
The 29.5cm diameter disk rotates counterclockwise on an axle through its center. F1=20.8N, F2=58.6N, F3=58.6N, F4=20.8N, and d=5.27cm. What is the net torque about the axle? Let the counterclockwise direction be positive.
Homework Equations
Torque = force (perpendicular) x distance (from pivot point)
The Attempt at a Solution
F1 = 0 N*m
F2 = 58.6 N x 0.1475m = -8.6435 N*m (clockwise)
F3 = 0.0527m x 58.6 sin45 N = 2.627777283 N*m (counterclockwise)
F4 = 0.0527m x 20.8 N = 1.09616 N*m (counterclockwise)
Therefore torque is -4.9196 N*m.
However that is apparently not the answer... What am i doing wrong? :/