cyturk
- 8
- 0
I am trying to solve an IVP problem and I seem to be stuck on it because I am getting an integration that seems very complicated and I think I messed up on it, I have my work so far below.
Find the solution to the IVP
ty^'+7y=2t^2 e^2t, y(1)=7
Is this equation linear? Determine in what interval the solutions exist.
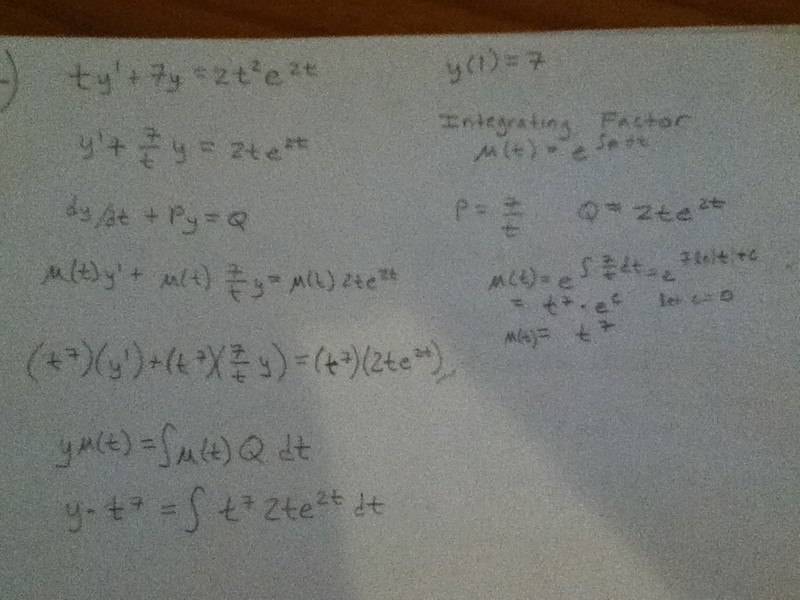
The image has my work so far, as you can see the integration for (t^7)(2te^2t) is a beast and that is why I think I am wrong so far. Here is the integration answer http://www.wolframalpha.com/input/?i=integrate+%28t^7%29%282te^%282t%29%29.
Homework Statement
Find the solution to the IVP
ty^'+7y=2t^2 e^2t, y(1)=7
Is this equation linear? Determine in what interval the solutions exist.
Homework Equations
The Attempt at a Solution
The image has my work so far, as you can see the integration for (t^7)(2te^2t) is a beast and that is why I think I am wrong so far. Here is the integration answer http://www.wolframalpha.com/input/?i=integrate+%28t^7%29%282te^%282t%29%29.