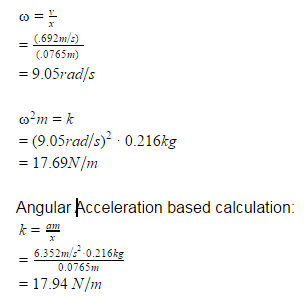Finding the Spring Constant: Angular Velocity vs Hooke's Law

[Robert Hilderman]

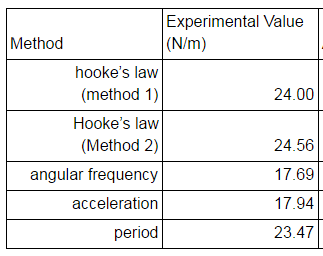
So I'm doing an experiment where I am using five different methods to find the spring constant of a spring. These three values of k should be the same but alas, they are not :( and I am at a loss as to why. The first method was by using hooke's law and finding the displacement and graphing the applied force over displacement (I called this method 1 in the picture below). Method 2 was oscillating the spring attached to a force sensor and having a position sensor under it. I graphed Force over Position (I had the force sensor zeroed at the spring's equilibrium so "position" was the spring's displacement). Method 5 was timing the period of the oscillation and plugging that into k=4pi^2m/T^2. All these methods gave a similar experimental value of k. However, when I used the position vs. time data to find k using angular velocity/acceleration, my values were 25% lower. My calculations are in the picture below. I used the maximum displacement, velocity, and acceleration values which were derived from the graphs. What I'm wondering is 1) did I do something wrong? and if not 2) what assumption is made that makes these values so off. Thank you so much. (In the picture, I accidentally called angular velocity "angular frequency". My bad)

 

[haruspex]

I assume 0.0765m is the amplitude of oscillation. How did you measure acceleration?
I don't understand the v/x calculation. The x seems to be the amplitude again, but what is v here? The max velocity? If so, how measured?
What value did you measure for the period?

Edit: why do you refer to angular velocity and angular acceleration? Isn't this just a mass bouncing up and down on the end of a suspended spring?
Any idea what the mass of the spring was?