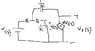
SUMMARY
The forum discussion focuses on finding the transfer function for a circuit using Kirchhoff's Voltage Law (KVL) and current analysis. The equation provided is Vi(s) = (I1*R) + (I3*R) + Vc(s), where Vc(s) = V0(s)/μ. Participants emphasize the importance of clarifying circuit parameters, such as the ground symbol and values for μ, to accurately derive the transfer function. The discussion concludes with a successful resolution after redrawing the circuit for clarity.
PREREQUISITES
- Understanding of Kirchhoff's Voltage Law (KVL)
- Familiarity with voltage-controlled voltage sources (VCVS)
- Basic circuit analysis techniques, including mesh and nodal analysis
- Knowledge of transfer functions in control systems
NEXT STEPS
- Study the Sallen-Key topology for filter design
- Learn about the application of KVL and KCL in circuit analysis
- Explore transfer function derivation techniques in electrical engineering
- Review Ohm's Law and its application in circuit problems
USEFUL FOR
Electrical engineers, circuit designers, and students studying control systems who need to understand transfer function derivation and circuit analysis techniques.