Finding the Work of a spring and friction with a changing angle

[titansarus]

Homework Statement

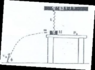
We shot a projectile with mass $m$ and velocity $v_0$ with angle $\phi$ it collide with a box with mass $M$ at the maximum height of its path. Then, they both start to move with another speed. (We define $t=0$ at this time) (Completely Inelastic Collision). The box is also connected to a spring from the ceiling with spring constant $k$ and the table has kinetic friction coefficient $\mu_k$. At the time $t=t_0$ it stops for a moment and then move backward (because of spring force). We want to find these:
(The angle of spring will be small so $sin\theta = tan\theta = \theta$ and $cos \theta = 1 - \theta^2 /2$

I) Work done by spring from from $0$ to $t_0$.

II) Work done by friction from from $0$ to $t_0$.

III) FInd an equation to find the position at time $t_0$. (Solving it is optional)

Homework Equations

$f = -k x$
$dw = \vec f . d\vec r$
$f = \mu_k N$
$sin\theta = tan\theta = \theta$ and $cos \theta = 1 - \theta^2 /2$

The Attempt at a Solution

I can find the velocity at t=0: $m v_0 cos \phi = (m + M) v$ so $v = v_0 cos\phi m/(m+M)$.

I can also say that $f_{spring} = -k\Delta x = k (L - L / (1 - \theta^2 /2)) = -k L (\theta^2 /2) / (1- \theta^2 /2)$

and $f.dr = f.dx = - k L (\theta^2 /2) /(1- \theta^2 /2) sin \theta L d\theta = - k L^2 (\theta^3 /2) /(1- \theta^2 /2) d\theta$

But I cannot find where velocity gets zero ($t = t_1$) to find the $\theta$ needed for integration.
Maybe I am getting the problem more complicated that it is? I don't know, maybe no integration is needed because $\theta$ is small enough that we can say it is equal to $d\theta$.
So what do I do?

 

[kuruman]

The speed becomes zero when all the kinetic energy immediately after the collision is converted to potential energy and work done by friction. That will give you a connection between $\theta_{max}$ and $v_0$. You need to rethink your potential energy. Start from $\Delta x=\sqrt{L^2+x^2}-L$, expand the first term for small values of $x$.

On Edit: Here $x$ is the horizontal displacement of the mass on the table and \Delta x is the amount by which the spring stretches. It's an unfortunate choice because the two are along two different directions.

 

[titansarus]

The speed becomes zero when all the kinetic energy immediately after the collision is converted to potential energy. That will give you a connection between $\theta_{max}$ and $v_0$. You need to rethink your potential energy. Start from $\Delta x=\sqrt{L^2+x^2}-L$, expand the first term for small values of $x$ and then connect $x$ to $\theta$.

I think it gets to $\Delta x =L (1 + x^2/L^2)^{1/2} - L \approx x^2 /2L^2 = \theta^2 /2$
But we also have friction work so maybe, $0.5 m v^2 = 0.5 k (\theta^2 /2)^2 + (m+M)g \mu_k L \theta$. now the problem is solving this equation. the equation is 4th degree polynomial and no calculator or something like WolframAlpha was allowed in the exam. What to do now?

 

[kuruman]

I think it gets to $\Delta x =L (1 + x^2/L^2)^{1/2} - L \approx x^2 /2L^2 = \theta^2 /2$
But we also have friction work so maybe, $0.5 m v^2 = 0.5 k (\theta^2 /2)^2 + (m+M)g \mu_k L \theta$. now the problem is solving this equation. the equation is 4th degree polynomial and no calculator or something like WolframAlpha was allowed in the exam. What to do now?

Not so fast.
1. The initial kinetic energy is $\frac{1}{2}(m+M)v^2$ because the masses stick together, no?
2. The potential energy you have is dimensionally incorrect because it has units of $k$. If the spring stretches by $\xi$ (my new name for $\Delta x$), what is the potential energy stored in the string? Once you find that, then you can write it in terms of $\theta$.
3. The force of friction is not constant because the normal force changes as the spring stretches. You have to find how and do an integral to find the work done by friction.

 

[haruspex]

Then, they both start to move with another speed. (We define t=0 at this time) (Completely Elastic Collision

If they continue with a common speed then it is a completely inelastic collision.

 

[titansarus]

Not so fast.
1. The initial kinetic energy is $\frac{1}{2}(m+M)v^2$ because the masses stick together, no?
2. The potential energy you have is dimensionally incorrect because it has units of $k$. If the spring stretches by $\xi$ (my new name for $\Delta x$), what is the potential energy stored in the string? Once you find that, then you can write it in terms of $\theta$.
3. The force of friction is not constant because the normal force changes as the spring stretches. You have to find how and do an integral to find the work done by friction.

The initial energy was a typo.

$U_{spring} = (1/2) k \xi^2$. And yes, I forgot to multiply it by L, it is actually $0.5 k (L \theta^2 / 2)^2$

For friction, it is actually $(mg - k L (\theta^2 /2) (1-\theta^2 /2))\mu_k$
I named $\theta_max = \alpha$
so work is $\int_0^\alpha (mg - k L (\theta^2 /2) (1-\theta^2 /2))\mu_k L d\theta = mgL\mu_k \alpha - kL^2\mu_k \alpha^3/6 + kL^2\mu_k \alpha^5 / 20 = C$ (If I didn't do any math mistakes). And even we don't know what is $\alpha$ actually!

Now the Energy Equation gets to $0.5 (m+M) v^2 = 0.5 k (L \theta^2 / 2)^2+ C$. solving this will actually give me the $\alpha$ in terms of $\alpha$! and solving that 5th degree polynomial to get the $\alpha$ itself is harder than 4th degree and I think there is not necessarily an algebraic way to solve it. So maybe there is an easier way to get $\alpha$. the problem must not get that hard.

 

[titansarus]

If they continue with a common speed then it is a completely inelastic collision.

Yes, you're right. I translated the question and I made this mistake in translating technical terms.

 

[kuruman]

$U_{spring} = (1/2) k \xi^2$. And yes, I forgot to multiply it by L, it is actually 0.5k(Lθ2/2)2

If $U_{spring} = (1/2) k \xi^2$ and the corrected value in post #3 should be $\Delta x=\xi=L\theta^2/2$, what is $U_{spring}$ in terms of $\theta$?

 

[titansarus]

If $U_{spring} = (1/2) k \xi^2$ and the corrected value in post #3 should be $\Delta x=\xi=L\theta^2/2$, what is $U_{spring}$ in terms of $\theta$?

U= 0.5 k (L \theta^2 / 2)^2.

I used this in the above solution. However, the friction get the equation so complicated.

 

[kuruman]

Start from the beginning because the spring force is not linear in $\theta$. The force exerted by the spring is $F=-k\xi$ along the spring. If the spring stretches by amount $d\xi$, the incremental work done by the spring is $dW = -k\xi~d\xi$. If you wish to introduce $\theta$, you need to find the incremental work in $\theta$ first (what is $\xi~d\xi~$in terms of $\theta$?) and then integrate.

However, the friction get the equation so complicated.

It's not a simple problem.

 

[titansarus]

Start from the beginning because the spring force is not linear in $\theta$. The force exerted by the spring is $F=-k\xi$ along the spring. If the spring stretches by amount $d\xi$, the incremental work done by the spring is $dW = -k\xi~d\xi$. If you wish to introduce $\theta$, you need to find the incremental work in $\theta$ first (what is $\xi~d\xi~$in terms of $\theta$?) and then integrate.

It's not a simple problem.

It is $\xi = L \theta^2 /2$ so $d\xi = L \theta d\theta$. So $W = \int - k L^2 \theta^3 /2 d\theta = -k L^2 \theta^4 / 8$ and I think it is the same as above, is it Wrong?

 

[kuruman]

It is $\xi = L \theta^2 /2$ so $d\xi = L \theta d\theta$. So $W = \int - k L^2 \theta^3 /2 d\theta = -k L^2 \theta^4 / 8$ and I think it is the same as above, is it Wrong?

It's not wrong. I thought it might be different, but it isn't. What about the work done by friction? What is the normal force?

 

[titansarus]

It's not wrong. I thought it might be different, but it isn't. What about the work done by friction? What is the normal force?

I wrote that in the above post: #6

$U_{spring} = (1/2) k \xi^2$. And yes, I forgot to multiply it by L, it is actually $0.5 k (L \theta^2 / 2)^2$

For friction, it is actually f= $(mg - k L (\theta^2 /2) (1-\theta^2 /2))\mu_k$
I named $\theta_{max} = \alpha$
so work is $\int_0^\alpha (mg - k L (\theta^2 /2) (1-\theta^2 /2))\mu_k L d\theta = mgL\mu_k \alpha - kL^2\mu_k \alpha^3/6 + kL^2\mu_k \alpha^5 / 20 = C$ (If I didn't do any math mistakes). And even we don't know what is $\alpha$ actually!

Now the Energy Equation gets to $0.5 (m+M) v^2 = 0.5 k (L \theta^2 / 2)^2+ C$. solving this will actually give me the $\alpha$ in terms of $\alpha$! and solving that 5th degree polynomial to get the $\alpha$ itself is harder than 4th degree and I think there is not necessarily an algebraic way to solve it. So maybe there is an easier way to get $\alpha$. the problem must not get that hard.

 

[haruspex]

It is $\xi = L \theta^2 /2$ so $d\xi = L \theta d\theta$. So $W = \int - k L^2 \theta^3 /2 d\theta = -k L^2 \theta^4 / 8$ and I think it is the same as above, is it Wrong?

It seems to me that θ⁴ is smaller order than terms that have already been neglected in using the sin(θ)~θ approximation.

Does the question state that the spring starts relaxed?

 

[kuruman]

I wrote that in the above post: #6

Yes, I see it now. I think it would be OK to drop the second order term in the expression. By this I mean drop the $\alpha^5/20$ term because it is much smaller than $\alpha^3/6$. This simplifies things a bit, but solving for $\alpha$ is not that simple. Setting that aside, if the intent of the problem is to express (I) the work done by the spring, (II) the work done by friction and (III) the turning point in terms of time $t_0$, then the only way I see doing this is by solving$~m\frac{dv_x}{dt}=\sum F_x$ to get the time dependence. From the looks of it it's a damped anharmonic oscillator problem.

Does the question state that the spring starts relaxed?

I don't see how the normal force problem can be addressed if the spring is not relaxed initially.

 

[haruspex]

I don't see how the normal force problem can be addressed if the spring is not relaxed initially.

If it starts relaxed then there are really two independent problems here. The initial projectile phase becomes irrelevant. We just have a combined mass with a given initial velocity.
A possible alternative is that the mass attached to the spring is only just resting on the surface initially, so there is no normal force until the collision. But that just makes the equations uglier.

 

[kuruman]

If it starts relaxed then there are really two independent problems here. The initial projectile phase becomes irrelevant. We just have a combined mass with a given initial velocity.

Yes, I agree. The two halves are quite unbalanced as far as difficulty is concerned unless the author had a simpler solution in mind.

 

[titansarus]

Yes, I agree. The two halves are quite unbalanced as far as difficulty is concerned unless the author had a simpler solution in mind.

I don't know what is the real answer of the question. But I think it should be a lot simpler that this. The question is for students who just know very basic calculus and only read Chapter 1 - 8 of Fundamental of Physics (Halliday , Resnick, Walker), So maybe it must be solved a lot easier than this. maybe the author of the question wanted to use $\theta$ itself instead of $d\theta$ because it is said that $\theta$ is very small.

It seems to me that θ⁴ is smaller order than terms that have already been neglected in using the sin(θ)~θ approximation.

Does the question state that the spring starts relaxed?

I think it is safe to assume the spring is at relaxed state at first. The problem didn't directly said that but usually in other questions which were solved by my university's professor in the class, when the question didn't mention anything, he assumed that it is at relaxed state.

 

[haruspex]

I think it should be a lot simpler that this.

It is unclear just what approximation is to be made. The first order term in the acceleration is μmg (m being the total mass). I suggest interpreting the information about the small angle as meaning that the acceleration equation should have no terms higher than θ² (or x² if you work in terms of linear displacement).

From a cursory attempt, I suggest working with x, not θ. It seemed to avoid getting tangled up with $\dot\theta^2$ terms.

 

[kuruman]

The first order term in the acceleration is μmg (m being the total mass).

Is that obvious? μmg is the leading term in the contribution to the acceleration from friction. There is an independent contribution from the spring force which depends on the spring constant. If the spring is stiff enough, the masses will hardly accelerate.

 

[haruspex]

Is that obvious? μmg is the leading term in the contribution to the acceleration from friction. There is an independent contribution from the spring force which depends on the spring constant. If the spring is stiff enough, the masses will hardly accelerate.

Judging from the diagram, this is a normal linear spring, freely jointed at the top. It is not a leaf spring. For small θ, the extension is of order θ², and the resulting horizontal force of order θ³.
Indeed, for a sufficiently large k, the mass would lose contact with the horizontal surface before this restoring force becomes significant.

So, as I posted, the lead term is μmg, and the next term is the order θ² reduction in that due to the lift from the spring. The horizontal force from the spring comes in third place.

 

[haruspex]

Fwiw, here's what I get working in terms of linear displacement. m is the total mass and v the velocity just after collision.
Exact equations:
$T=Lk(1-\cos(\theta))$
$m\ddot x=-T\sin(\theta)-\mu (mg-T\cos(\theta))$
Approximations:
$\cos(\theta)=1-\frac 12(\frac xL)^2$
$\sin(\theta)=\frac xL(1-\frac 12(\frac xL)^2)$

$m\ddot x=-\mu m g+\frac{\mu k}{2L}x^2-\frac{k}{2L^2}x^3+O(x^4)$
Discarding x⁴ and higher, then integrating
$\frac 12 m\dot x^2=\frac 12mv^2-\mu mgx+\frac{\mu k}{6L}x^3-\frac{k}{8L^2}x^4$
Again, throwing away x⁵ and higher terms, we can get this into the form velocity *(quartic in x)=1, and integrate again to get: quintic in x = t.