Thetom
- 59
- 0
I need to make a net for a frustum. The following web page explains how to do it... http://www.analyzemath.com/Geometry/conical_frustum.html
I have tried but am unable to do this complicated, advanced (o.k basic) math.
In the following figure I have the values R,r and h.

R = 40
r = 35
h = 83
I need the values for x,y,t and H in the following figure so I can construct my net.
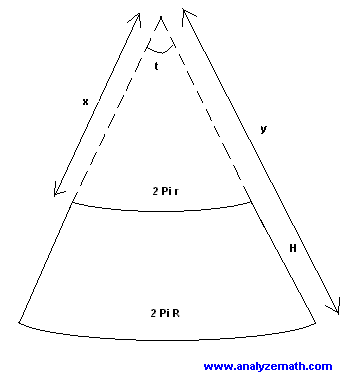
x = ?
y = ?
t = ?
H = ?
Can anyone please help me find x,y,t,H ?
I have tried but am unable to do this complicated, advanced (o.k basic) math.
In the following figure I have the values R,r and h.
R = 40
r = 35
h = 83
I need the values for x,y,t and H in the following figure so I can construct my net.
x = ?
y = ?
t = ?
H = ?
Can anyone please help me find x,y,t,H ?
Last edited: