Koko23
- 3
- 0
- Homework Statement
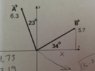
- Vector C is given by C=B-A. The magnitude of vector A is 6.3 units and 23 degrees from the y axis in quadrant II. The magnitude of vector B is 5.7 units and 34 degrees from the x axis in quadrant I. What is the magnitude of vector C? What is the angle measured from the x axis to vector C in degrees?
- Relevant Equations
- Law of Cosine and Sine
Ax=6.3 cos 23; Ay=-6.3 sin 23; Bx= 5.7 cos 34; By=5.7 sin 34. Is this correct to calculate vector C magnitude which I got 7.7 units. Also is vector C in quadrant IV?
I am not sure how to calculate the angle part of this question.
I am not sure how to calculate the angle part of this question.