Jacobpm64
- 235
- 0
Homework Statement
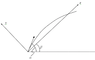
If a projectile is fired from the origin of the coordinate system with an initial velocity v_0 and in a direction making an angle \alpha with the horizontal, calculate the time required for the projectile to cross a line passing through the origin and making an angle \beta < \alpha with the horizontal.
Homework Equations
\mathbf{F} = m \mathbf{\ddot{r}}
tan(\theta) = \frac{y}{x}
The Attempt at a Solution
So, here I go. First, I treated the x-direction and y-direction separately.
x-direction
I know that there is no acceleration in the x-direction so,
\ddot{x} = 0
Assuming that x = y = 0 at t = 0 because the projectile is fired from the origin, we get (by integrating)
\dot{x} = v_{0} cos(\alpha)
x = v_{0} t cos(\alpha)
y-direction
We only have one acceleration in the y-direction (gravity).
\ddot{y} = -g
By integrating , we get:
\dot{y} = -gt + v_{0} sin(\alpha)
y = \frac{-gt^2}{2} + v_{0} t sin(\alpha)
Now is where my confusion starts. I suppose I need to solve something of the form arctan(\frac{y}{x}) < \alpha for t.
When substituting for y and x and doing some algebra, I get:
arctan(\frac{2v_{0}sin(\alpha) - gt}{2v_{0}cos(\alpha)}) < \alpha
Is there any way to solve this for t? Or, is there another way of working this problem that I am not seeing?
It's been quite a long time since I've worked with mechanics, and this is my first upper-level mechanics course, so I don't really know what I'm dealing with here.
Any help is appreciated. Thanks in advance.