- #1
david3305
- 6
- 0
Homework Statement
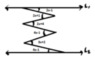
Find x. L1 and L2 are parallel
choices:
a)2°40'
b)2°30'
c)2°45'
d)2°15'
e)2°20'
Homework Equations
Σleft∠ = Σright∠
The Attempt at a Solution
2x+1+4x-1+4x-1 = 2x-1+2x+4+3x+2
10x-1=7x+5
3x=6
x=2°
Not sure how the answers include minutes '
Maybe I'm overlooking something?