Finite difference problem

[Anonymous119]

I found this part of forum the most relevant to this theme so excuse me if I missed.

This year I'm doing a high school summer project related to quantum mechanics. Anyway I'm using finite difference method to solve Schrödinger equation. Before starting to work on a project I decided to get some practice so here is the problem that I am trying to do.

I'm trying to find energies and wave function for electron in 2D circle potential well.
Wave function outside is zero and inside It is determined by Schrödinger equation.
And here is my procedure:

1. Divide space into point separated by distance h (see the picture)
2. Write Laplacian in point ψ(x,y) by It's neighbors and It looks like for example

d^2ψ(x,y)/dx^2 = [ψ(x-h,y)-2*ψ(x,y)+ψ(x+h,y)]/h^2

Also here is the correction for boundary conditions for example if I am looking at the point (x,y) where (x+h,y) is out of the well: i find distance ε so that the point (x+ε,y) is exactly on the boundary and i write d^2ψ(x,y)/dx^2 in terms of ψ(x-h,y), ψ(x,y), ψ(x+ε,y), h and ε. I derive the formula using Taylor series around (x,y) and taking terms up to h^2 or ε^2. Now i have ψ(x+ε,y)=0 and formula is:

d^2ψ(x,y)/dx^2=-2*ψ(x,y)/ε/h+2*ψ(x-h,y)/h/(h+ε)

3. Putting all coefficients in the Hamiltonian using MATLAB i calculate eigenvalues and eigenvectors.

And finally here is the problem i found on the internet that energy should be going like this E1=5.8*E0, E2=14.7*E0, E3=26,4*E0, E4=30,5*E0 and so on...(http://www.st-andrews.ac.uk/physics...s/2DCircularWell/infinite circular well5.html CHECK CONTROLS AND SHOW ENERGY TO SEE)

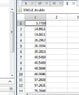
And here are my results

As you can see i got this values for energy but there are many others wrong energies also i got some complex energy :(. The wave function has some points where the value is 10^10 times bigger than normally.

I don't have much experience so I ask if anyone can help me to see what is wrong here. It will be significantly if anyone can see is mistake in a theory or it could be in a code.

Thanks!

 

[soarce]

Assuming that there is no error in your implementation you can perform a quick check: double the number of sample points simultaneously in x and y and see how the eigenvalues are shifting. As the energy is increasing the values should display a larger shift, in this way you can determine which values you should trust and which don't. For large energy values and wavefunctions of complex structure (nodes, angular momentum etc) one should increase the number of sample points (or decrease the spatial step h).
This fact is due to the discretization of a continuous system, the eigenvalues you get are only approximate values or even spurious values (i.e. values which don't correspond to any eigenvalues of the continuous equation). In your case, for instance, the complex eigenvalues. The task of discriminating the spurious eigenvalues from physical ones is not trivial and requires some practice. I didn't work with finite diferences, but I came across this problem using spectral methods. I can recommend you the sections 7.5 and 7.6 from Boyd's book Spectral metods where he discuss some criteria for rejecting spurious and unphysical eigenvalues. Maybe they can help you.

PS: other thing that you can do to minime the numerical errors is to take advantage of the symmetry of the equation, e.g. if you look for radial symmetric solutions then use polar coordinates instead of cartesian ones.