Discussion Overview
The discussion focuses on finding resources and guidance for setting up Finite Element Analysis (FEA) in MATLAB. Participants share book recommendations, code references, and personal experiences related to implementing FEA and Computational Fluid Dynamics (CFD) methods.
Discussion Character
- Exploratory
- Technical explanation
- Homework-related
Main Points Raised
- One participant seeks a detailed textbook to assist in coding FEA in MATLAB, mentioning their background in hand sketches.
- Another participant recommends a book with MATLAB code and notes that an older book may still be relevant despite changes in MATLAB since its publication.
- A different participant shares a link to a resource that claims FEA can be implemented in MATLAB in 50 lines, suggesting starting with a finite difference method for beginners.
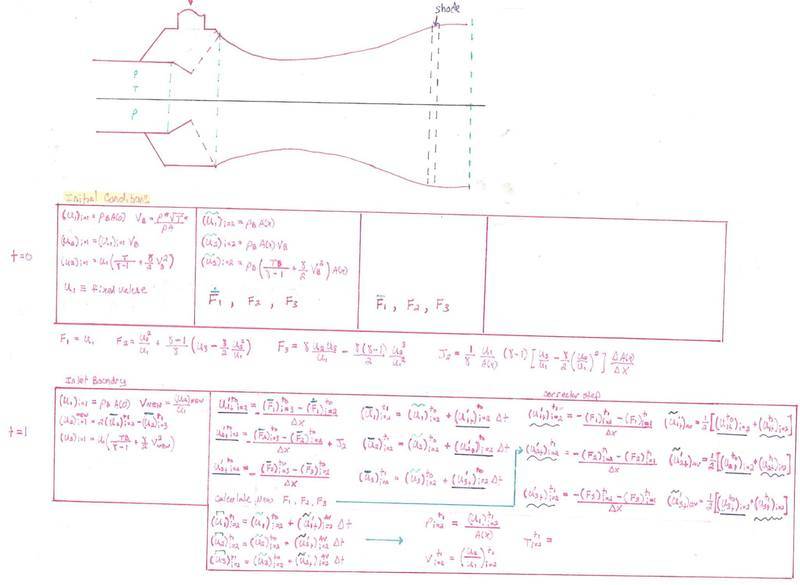
- One participant reflects on the numerical methods presented in John Anderson's book, noting its effectiveness in breaking down PDEs into algebraic problems necessary for FEA.
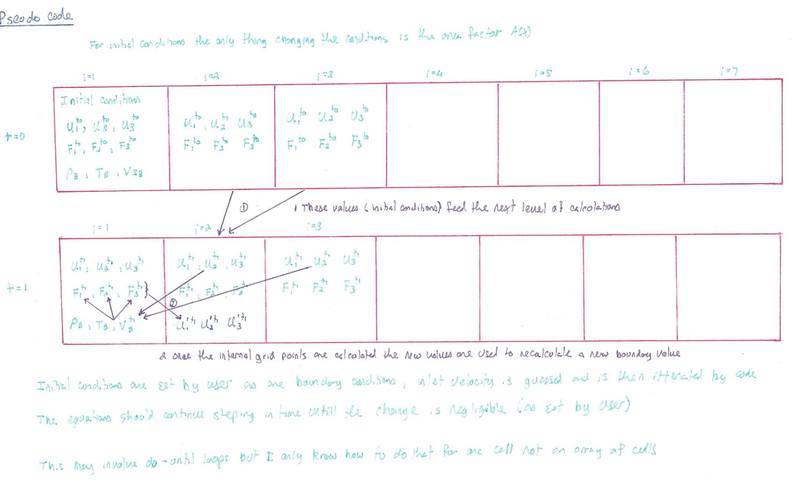
- Another participant describes their approach to defining and looping through arrays in MATLAB, detailing the process of handling initial and boundary conditions and the iterative nature of their calculations.
- Participants express uncertainty about the availability of good finite element method textbooks and share personal collections of books on the topic.
Areas of Agreement / Disagreement
There is no consensus on a single best resource for learning FEA in MATLAB, with multiple book recommendations and approaches discussed. Participants have differing views on the relevance of older texts and the best methods to implement FEA.
Contextual Notes
Some participants mention the need for further clarification on specific coding techniques and the handling of arrays in MATLAB, indicating that their understanding is still developing.
Who May Find This Useful
Individuals interested in learning about FEA in MATLAB, particularly those with a background in computational methods or fluid dynamics, may find this discussion beneficial.