- #1
simplex
- 40
- 0
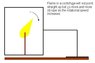
Flame in a centrifuge will go oblique (nearly parallel to the ground if the device is spinning extremely fast).
Flame in a centrifuge will not point straight up but go more and more oblique as the rotational speed increases (see the picture)
Experiment:
1) Put a candle in a preferably sealed container, or even one that has a few small holes on its top and bottom to avoid starving the flame of oxygen too fast.
2) Lit the candle, close the jar and rotate it.
The flame should go more and more oblique as the speed increases (see the picture).
NOTE: The position of the flame has nothing to do with blowing air on it from one side because the container is sealed.
Source: << Link deleted by berkeman >>
QUESTION: Will the flame really go oblique?
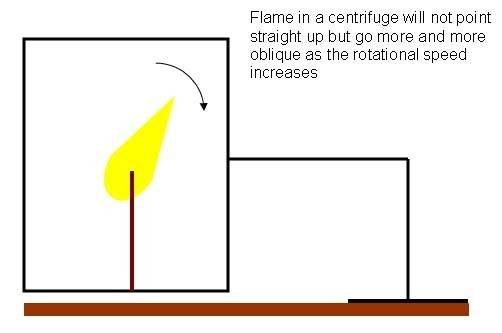
Flame in a centrifuge will not point straight up but go more and more oblique as the rotational speed increases (see the picture)
Experiment:
1) Put a candle in a preferably sealed container, or even one that has a few small holes on its top and bottom to avoid starving the flame of oxygen too fast.
2) Lit the candle, close the jar and rotate it.
The flame should go more and more oblique as the speed increases (see the picture).
NOTE: The position of the flame has nothing to do with blowing air on it from one side because the container is sealed.
Source: << Link deleted by berkeman >>
QUESTION: Will the flame really go oblique?
Attachments
Last edited by a moderator: