Frankenstein19
- 56
- 0
Homework Statement
Homework Equations
The Attempt at a Solution
[/B]
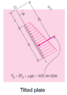
1. By resultant force, does that mean the force exerted on the side of the water + force exerted on side of the oil? Because I'd think that the force on the side of the water would be different than the force exerted on the door on the side of the oil.
2. When I find the force exerted by the oil, I multiple the SG of the oil by the density of water to get the specific weight of the oil, but in chegg solutions I've been seeing people use 31.75lb/ft^3 and saying that's the specific weight of AIR. Can I use the density of water?
3. When finding the force exerted by the water on the door, I should be considering the 10psig of the air, right?
4. When finding Ixx, I should consider the way the door will open, right? How do I know which way it'll open? I was taking b=12 for Fr so I carried that convention when doing Ixx and used 1/12ba^3 instead of 1/12b^3a which was what I was seeing in the chegg solutions.
Any help is greatly appreciated.
Attachments
Last edited by a moderator: