Force acting on a stationary object in a flowing pipe

[ykh-1992]

Greetings everyone,

I've been recently trying to calculate the forces acting on a stationary object in pipe with flowing fluid. I've returned to my college textbooks to get some help and I've found examples that clearly demonstrated how to accomplish just that.

Below is one example.
This example uses conservation of momentum principles for a simple incompressible, inviscid fluid which is what I'm looking for.

Now I've got to thinking.
If the plug in the example was reduced in diameter, then intuition tells me that the force to hold the plug stationary would be smaller.
So I tried using a smaller plug diameter in the formula but I got a larger force!

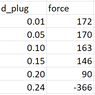
See the table below.
Keeping everything else the same, as the plug diameter decreases, the force to hold it in place increases.

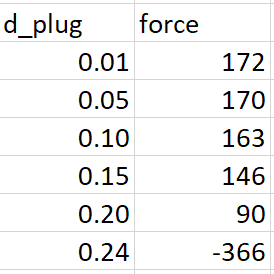
It's either the author of the textbook has understood this calculated force incorrectly or this is actually real and my understanding of the world is wrong.
There is another example later in the textbook which is solved in the same method so it is not a one-off type or something.

Does anyone know what is happening here? And is the correct method to determine the force to keep a plug stationary in a pipe with flowing fluid?

Thanks,

 

[Chestermiller]

In this example, the upstream pressure they give is not compatible with the Bernoulli equation. Bernoulli indicates that the upstream pressure should be 3.133 MPa (rather than 3.5 MPa). So there is already something wrong with their analysis.

In the calculations for the other plug diameters, one needs to recalculate the upstream pressure using Bernoulli, given the new values of the downstream velocity. So, as the plug gets smaller, so does the upstream pressure. I assume that you did not update the upstream pressures in your calculations.

 

[Delta2]

In this example, the upstream pressure they give is not compatible with the Bernoulli equation. Bernoulli indicates that the upstream pressure should be 3.133 MPa (rather than 3.5 MPa). So there is already something wrong with their analysis.

In the calculations for the other plug diameters, one needs to recalculate the upstream pressure using Bernoulli, given the new values of the downstream velocity. So, as the plug gets smaller, so does the upstream pressure. I assume that you did not update the upstream pressures in your calculations.

At first glance, I don't understand why the upstream pressure should change. Seems to me that upstream pressure is just an initial condition for the problem, and that it depends on the source/pump that generates the upstream, and generally in what happens in the upstream network.

 

[Chestermiller]

At first glance, I don't understand why the upstream pressure should change. Seems to me that upstream pressure is just an initial condition for the problem, and that it depends on the source/pump that generates the upstream, and generally in what happens in the upstream network.

Are you not comfortable with the Bernoulli equation? In this case, the upstream pressure is necessary to increase the kinetic energy per unit mass of the fluid from the inlet value to the outlet value. it depends, not on what is happening upstream, but what is happening downstream. If your upstream network applied a higher upstream pressure, all that would just mean would be that the volumetric flow rate would have to be higher. For a given setup, there is a one-to-one relationship between the upstream pressure and the flow rate.

 

[Delta2]

Are you not comfortable with the Bernoulli equation? In this case, the upstream pressure is necessary to increase the kinetic energy per unit mass of the fluid from the inlet value to the outlet value. it depends, not on what is happening upstream, but what is happening downstream. If your upstream network applied a higher upstream pressure, all that would just mean would be that the volumetric flow rate would have to be higher. For a given setup, there is a one-to-one relationship between the upstream pressure and the flow rate.

I ll have to ask you kindly how you apply Bernoulli here and why at first place you also said that the upstream pressure should be 3.133MPa. Your portion of text that I highlighted in red sounds like some sort of reversed causality to me.

 

[Chestermiller]

I ll have to ask you kindly how you apply Bernoulli here and why at first place you also said that the upstream pressure should be 3.133MPa. Your portion of text that I highlighted in red sounds like some sort of reversed causality to me.

Bernoulli applied:
$$p_1+\frac{1}{2}\rho v_1^2=p_2+\frac{1}{2}\rho v_2^2$$ with $p_2$ equal to 0 (gauge pressure). See what you get for $p_1$, the upstream gauge pressure, from this Bernoulli calculation application.

 

[Delta2]

I see, the way I applied it, was to consider $p_1$ as depending on the upstream and given as initial value, and calculate $p_2=p_2(p_1,v_1,v_2)$.

So (novice question to follow) what is gauge pressure and why we identically set it to 0 (and this is essentially our initial value, not p_1). This gauge pressure term implies a reverse causality I think where the gauge pressure which is the downstream pressure determines the upstream pressure.

 

[Chestermiller]

I see, the way I applied it, was to consider $p_1$ as depending on the upstream and given as initial value, and calculate $p_2=p_2(p_1,v_1,v_2)$.

So (novice question to follow) what is gauge pressure and why we identically set it to 0 (and this is essentially our initial value, not p_1). This gauge pressure term implies a reverse causality I think where the gauge pressure which is the downstream pressure determines the upstream pressure.

Gauge pressure is just absolute pressure minus atmospheric pressure. For incompressible flow systems, it is just a convenient parameter with which to work.

Do you accept the Betnoulli equation as describing the flow behavior of inviscid fluids, or don’t you? If you do, then you must accept that the downstream pressure boundary condition and the volumetric flow rate determines the upstream pressure. If the fluid were significantly viscous, would you still have the same doubts?

 

[Delta2]

Do you accept the Betnoulli equation as describing the flow behavior of inviscid fluids, or don’t you? If you do, then you must accept that the downstream pressure boundary condition and the volumetric flow rate determines the upstream pressure.

Yes I accept these, but I have a minor doubt regarding the setting of $p_2$ identically to zero, regardless of what happens (if we change the object diameter, or apply more pressure from the upstream e.t.c.). I got an intuition feeling that $p_2$ , in reality, would be small but variable and would depend on the object diameter, the volumetric flow rate, and the upstream pressure.

 

[Chestermiller]

Yes I accept these, but I have a minor doubt regarding the setting of $p_2$ identically to zero, regardless of what happens (if we change the object diameter, or apply more pressure from the upstream e.t.c.). I got an intuition feeling that $p_2$ , in reality, would be small but variable and would depend on the object diameter, the volumetric flow rate, and the upstream pressure.

The pipe discharges to the atmosphere, so the exit gauge pressure is zero. Pressure is continuous at the radial interface between fluid and air. And, by Pascal's law, pressure is isotropic within the fluid, so it is equal in all directions. So the fluid force per unit area pointing opposite to the flow of the fluid at the pipe exit is atmospheric pressure (zero gauge).

Have you not done any problems (Torricelli problems) where liquid discharges through a hole in the side of a tank? The fluid pressure at the exit hole is atmospheric, right?

Your intuition is doing you a disservice, and I recommend getting more practice solving Bernoulli problems.

 

[Delta2]

You got me Chet, I haven't solved many Bernoulli problems...

 

[ykh-1992]

Thanks for the information, Chestermiller and Delta. I'm sure the example shown was to demonstrate how to calculate the force acting on the plug and that's why the upstream pressure is a little off.
But my concern is that the method applied to calculate the force acting on the plug does not seem right.

Let me give this example, if we were to fix a plug in a large enough pipe or channel where the upstream and downstream pressures around the plug are equal, there should still be a force acting on that plug simply because there is flow striking the face of the plug (like putting your hand in a flowing river or out of a car window).
Now, if I were to change the size of the pipe or channel to be bigger or smaller while keeping the upstream fluid velocity the same, the force acting on the plug according to the example would still change! And that is my problem.

Take a look at the equation they've used in the example.​

A1 is the area of the pipe and A2 is the area of the annulus. The force calculated makes sense if I'm trying to figure out the forces acting on the fluid in the control volume but not on the plug alone. The formulation of the equation states that the area of the pipe alone (A1) will change the force acting on the plug even if I hold the fluid velocity (V1) the same.

It's like the textbook is telling me that if I put my hand in two rivers with the same fluid velocity but with different widths, then I would feel different forces which doesn't make sense.
In both case I should feel the same force since its the same hand and same fluid velocity--it shouldn't matter the width of the river.

It makes sense to me that we take the force acting on the plug due to striking flowing fluid to be as follows.

With the second equation, no matter the size of the pipe or channel surrounding the plug, all that matters is the fluid velocity striking the plug and the size of plug itself.
This would agree with the rivers analogy.

I hope this clarifies my concern with the example's equation as I find it to be misleading.
So, is my line of thinking correct? Or have I assumed something incorrect here?Thanks,

 

[Delta2]

What are the results you get regarding the force ,if you keep updating the $p_1$ pressure (which will become smaller as diameter gets smaller) whenever you change the diameter of the plug?

I think the second equation you wrote and which resembles greatly the equation $F=-kv^2$ is correct only when you have the plug completely submerged into the stream, but in the example in post 1, we have fluid from one side of the plug, and air from the other side of the plug. I think that's the key difference.

 

[ykh-1992]

Delta, I think you're right about the plug being half-submerged.
But allow me to continue to demonstrate with one more example just to be sure.

Here I'm changing the diameter of the pipe such that the upstream velocity and pressure remain the same.
Since the plug diameter, the striking fluid velocity, and differential pressure across the plug are the same, I should expect the force acting on the plug to be the same as well.
However, the equation from the example tells me that the force should increase which is against intuition.
I anticipate the graph below to remain constant over pipe ID but this is not the case.

Based on the graph above, if I put my hand out of a car window driving at 40 mph, I will feel more force in an open road compared to the same scenario inside a tunnel.
Is this result sensible?Thanks,

 

[Chestermiller]

If you put your hand or an object in a stream of inviscid fluid, inviscid flow theory predicts that the drag force on your hand is zero. For example, flow of an inviscid fluid past a submerged sphere or cylinder will be such that the pressure variations on the back side of the object exactly match the pressure variations on the front side of the object, so that the net force is zero. The drag equation that Delta^2 wrote only applies to fluids that have non-zero viscosities (including gases such as air). The reason that the drag is non-zero in a viscous fluid is that the fluid velocity must go to zero at the surface of the object, due to the non-slip boundary condition. This produces asymmetric distribution of pressure from front to back on the object in addition to producing shear drag on the sides of the object.

That being said, if the flow is inviscid in your problem, then two simultaneous equations apply for determining the two unknowns, upstream pressure and force on plug:
$$p_1=\frac{1}{2}\rho v_2^2-\frac{1}{2}\rho v_1^2\tag{1}$$
and
$$F_{plug}=p_1A_1+\rho (v_1^2A_1-v_2^2A_2)\tag{2}$$
subject to the constraint that $$v_1A_1=V_2A_2=Q$$
Eqn. 1 is Bernoulli's (mechanical energy balance) equation and Eqn. 2 is the macroscopic momentum balance equation.

See what you get if you solve these two equations to determine the force on the plug. You will find that the force increases as the size of the plug increases. Please share with us your graph for that.

 

[Chestermiller]

 

[ykh-1992]

If you put your hand or an object in a stream of inviscid fluid, inviscid flow theory predicts that the drag force on your hand is zero.

I think the second equation you wrote and which resembles greatly the equation F=−kv2F=−kv2F=-kv^2 is correct only when you have the plug completely submerged into the stream, but in the example in post 1, we have fluid from one side of the plug, and air from the other side of the plug. I think that's the key difference.

These two comments pretty much summarize what I've been asking about. Thank you gentlemen for your patience.
I've tried figuring out the force acting on a fully submerged plug using inviscid theory and when the net force came out as a zero, I thought I was doing something.

Here are the charts using eqs. 1 and 2.

So then I would like to ask, how does one go about calculating the forces acting on a fully submerged body in a pipe with viscous fluid? (similar to the plug example but fully submerged)
If I understand this correctly, there are two forces to account for: 1) momentum change, 2) pressure differential.

Did I get that right?

 

[ykh-1992]

Did I get that right?

Never mind. Apparently, Wikipedia has a good article on drag forces and drag coefficients.

I just would like to know if drag would account for a pressure differential induced by friction.
For example, if the annulus between a pipe and a plug is small enough to generate an appreciable pressure drop due to friction, would drag account for this behavior?

Also, if anyone has any good references (books or articles) on drag forces for simple cylinders, please share as that would be greatly appreciated.Thanks,

 

[Chestermiller]

These two comments pretty much summarize what I've been asking about. Thank you gentlemen for your patience.
I've tried figuring out the force acting on a fully submerged plug using inviscid theory and when the net force came out as a zero, I thought I was doing something.

Here are the charts using eqs. 1 and 2.
View attachment 228837

View attachment 228838

So then I would like to ask, how does one go about calculating the forces acting on a fully submerged body in a pipe with viscous fluid? (similar to the plug example but fully submerged)
If I understand this correctly, there are two forces to account for: 1) momentum change, 2) pressure differential.

View attachment 228840

Did I get that right?

To do it for a viscous fluid, you need to solve the full Navier Stokes equations for the velocity distributions and pressure distributions within the duct (and around the object).

 

[Chestermiller]

Never mind. Apparently, Wikipedia has a good article on drag forces and drag coefficients.

I just would like to know if drag would account for a pressure differential induced by friction.
For example, if the annulus between a pipe and a plug is small enough to generate an appreciable pressure drop due to friction, would drag account for this behavior?

Also, if anyone has any good references (books or articles) on drag forces for simple cylinders, please share as that would be greatly appreciated.Thanks,

The total drag force is equal to the force resulting from the pressure distribution (called form drag), including the coupling between inertia and viscous friction) and the force from viscous friction on the surface of the object. If the clearance between the plug and the duct is small enough, the pressure drop and drag force will be dominated by the viscous frictional shear stress at the outer surface of the plug. Look up "viscous flow in an annulus."

A great book on drag forces (and a plethora of other things) is Transport Phenomena by Bird, Stewart, and Lightfoot.

 

[ykh-1992]

Appreciate the immense help, Chestermiller and Delta^2.
I'll do some research on the subject and see if I can find something that will get me where I want to get.

Thanks,