link223
- 70
- 12
- Homework Statement
- So I just want to see which forc acts on the walking beam at E but itsn't quite obvious to me from the figure.
- Relevant Equations
- Structural Analysis
So.. question:
- How do I know that only the pin is at work at E and not those 2 beams? my guess: It is because those 2 beams are connected to the pin whilst the pin is the one that exerts a force on that walking beam DEF?
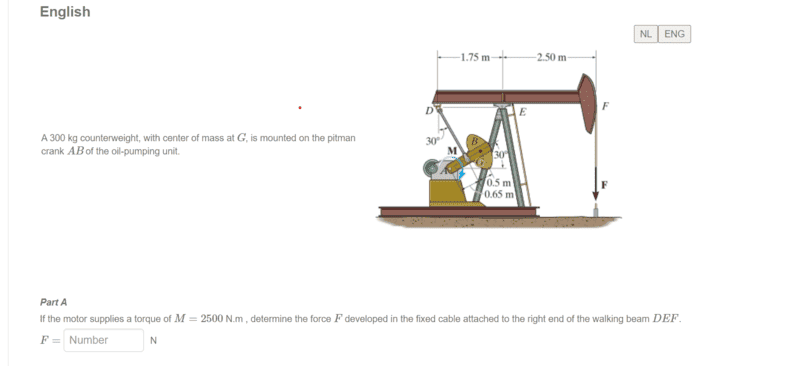
- How do I know that only the pin is at work at E and not those 2 beams? my guess: It is because those 2 beams are connected to the pin whilst the pin is the one that exerts a force on that walking beam DEF?