Reizor1989
- 1
- 0
First off, I want to apologize if anything is made unclear. I'm ultra-stressed right now, I'm sure I can get over this physics problem. I just need a layman's explanation of this.
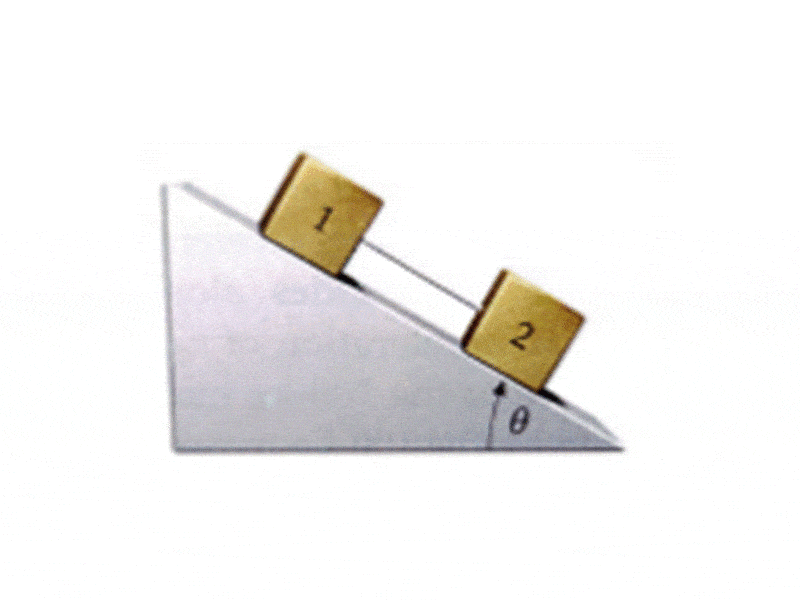
1. A taut massless string connects two boxes as shown below. The boxes are placed on an incline plane at θ = 33.00. What is the acceleration of boxes as they move down the incline, given m2 = 1.2 kg, m1 = 6.8 kg, μ2 = 0.10 and μ1 = 0.20
 . 2. Constructed free body diagram for M1 (mass 1) with normal force (n) along the positive y-axis, friction (f) along the negative x-axis, tension (T) along the positive x-axis, and Force of gravity (Fg) in quadrant IV, 33 degrees from the negative y-axis. (a=acceleration, mu=coefficient of friction)
. 2. Constructed free body diagram for M1 (mass 1) with normal force (n) along the positive y-axis, friction (f) along the negative x-axis, tension (T) along the positive x-axis, and Force of gravity (Fg) in quadrant IV, 33 degrees from the negative y-axis. (a=acceleration, mu=coefficient of friction)
a.) Summed forces of x as Fx = T - f + Fgx = M1*a ->
-> M1 * a - mu*n + M1*g = M1 * a
-> (This is where I think I'm screwing up. I want to isolate the first (a), but I have no idea how.)
b.) Summed forces of y as Fy = n - Fgy = M1 * a ->
-> n - Fgy = 0 (acceleration is 0)
-> n = Fgy
3. Constructed free body diagram for M2 (mass 2) with (n) along the positive y-axis, (f) along the negative x-axis, tension (T) along the positive x-axis, and Force of gravity (Fg) in quadrant IV, 33 degrees from the negative y-axis. (a=acceleration, mu=coefficient of friction)
a.) Same as 2a
b.) Same as 2b
4. Basically I have no idea where to go from here. Did I screw up on the diagram? Is something wrong with my algebra? What can I do next?
1. A taut massless string connects two boxes as shown below. The boxes are placed on an incline plane at θ = 33.00. What is the acceleration of boxes as they move down the incline, given m2 = 1.2 kg, m1 = 6.8 kg, μ2 = 0.10 and μ1 = 0.20
a.) Summed forces of x as Fx = T - f + Fgx = M1*a ->
-> M1 * a - mu*n + M1*g = M1 * a
-> (This is where I think I'm screwing up. I want to isolate the first (a), but I have no idea how.)
b.) Summed forces of y as Fy = n - Fgy = M1 * a ->
-> n - Fgy = 0 (acceleration is 0)
-> n = Fgy
3. Constructed free body diagram for M2 (mass 2) with (n) along the positive y-axis, (f) along the negative x-axis, tension (T) along the positive x-axis, and Force of gravity (Fg) in quadrant IV, 33 degrees from the negative y-axis. (a=acceleration, mu=coefficient of friction)
a.) Same as 2a
b.) Same as 2b
4. Basically I have no idea where to go from here. Did I screw up on the diagram? Is something wrong with my algebra? What can I do next?