Formulae for calculating the area of a quadrilateral non-cyclic

[Bruno Tolentino]

I want knows if a formula for calculate the area of a quadrilateral non-cyclic needs of just four values (the values of the four edges) or if is necesseray 6 values (the values of the four edges MORE os values of the two diagonals)?

This formula needs of 6 values (a,b,c,d,p,q):

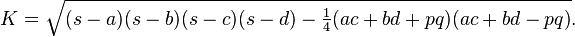
OBS: s = (a+b+c+d)/2

And this formula needs of just 4 (a,b,c,d):

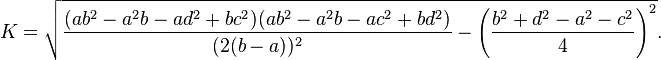
But, I tested this second formula in the geogebra and it don't works...

Sources:
http://en.wikipedia.org/wiki/Trapezoid#Area
http://en.wikipedia.org/wiki/Quadrilateral#Non-trigonometric_formulas
https://en.wikipedia.org/wiki/Bretschneider's_formula#Related_formulas

 

[mathman]

The four edges are obviously not sufficient. Start with a square (side length=1) - area =1. Now take a pair of diagonally opposite corners and move them toward each other, while keeping the side lengths constant. When they meet, the resultant quadrilateral area = 0.

 

[sjb-2812]

And 4 sides and 1 diagonal is not sufficient either. Consider a shape with sides 1, 1, 0.8, 0.8 in that order. Now the 0.8 v can be inside, or outside (convex or concave) with the area different.