Four L-shaped members: Mechanical Analysis Problem

[jojosg]

TL;DR: This determine the support reactions at A & B

I tried calculate moment about a which is 2a(By + Bx + Ey + Ex +F) + a (Gy + Gx + Cy + Cx). But I don't think I'm correct, any help would be appreciated, this was a question on a final exam paper in my Mechanics course.

 

[wrobel]

Try to write down the equations of equilibrium for each L-like rigid body. You have three scalar static equations for a rigid body in a planar problem.
There are 2 unknown components of a reaction in each hinge and 12 static equations for 4 rigid bodies.
The number of equations and the number of unknowns matches.

 

[jojosg]

Try to write down the equations of equilibrium for each L-like rigid body. You have three scalar static equations for a rigid body in a planar problem.
There are 2 unknown components of a reaction in each hinge and 12 static equations for 4 rigid bodies.
The number of equations and the number of unknowns matches.

Like this?

 

[Lnewqban]

Why are Bx and Ex being multiplied by 2a?

 

[jojosg]

Why are Bx and Ex being multiplied by 2a?

I took moment about A and the distance from A for Ex & Bx are 2a.

 

[Lnewqban]

I took moment about A and the distance from A for Ex & Bx are 2a.

What matters is the perpendicular distance between the pivot and the force.
That distance is zero for force Bx.
For force Ex is ...

 

[jojosg]

What matters is the perpendicular distance between the pivot and the force.
That distance is zero for force Bx.
For force Ex is ...

2a(By + Ey +F) + a (Gy + Gx + Cy + Cx + Ex) like this?

 

[Lnewqban]

2a(By + Ey +F) + a (Gy + Gx + Cy + Cx + Ex) like this?

Reconsider Gx.

 

[haruspex]

Like this?

You are missing a force at D on ADC. Likewise at E on CEB.

In your moment sums, you need to be clear on the system you are considering. Your expressions seem to be taking the whole system of the four L pieces, in which case:
- the forces at D, E, C and G are internal, so should be ignored,
- the perpendicular distance from Bx to A is zero,
- assuming By acts upwards on CEB, the moments from By and F act in opposite directions around A.

Listing Ax, Ay, Bx, … etc., you have 12 unknowns, so to find them all you need 12 equations. Horizontal and vertical force balance on each L piece gives you 8 equations, so you will need four more from moment balance. Apply moment balance to some individual L pieces.

Since you are only asked for forces at A and B, you may be able to avoid finding all 12 by careful choice of which balance equations to use.

 

[jojosg]

Reconsider Gx.

on second maybe this 2a(By + Ey - F - Gx) + a(Gy + Cy - Ex - Cx) = 0.

 

[jojosg]

You are missing a force at D on ADC. Likewise at E on CEB.

In your moment sums, you need to be clear on the system you are considering. Your expressions seem to be taking the whole system of the four L pieces, in which case:
- the forces at D, E, C and G are internal, so should be ignored,
- the perpendicular distance from Bx to A is zero,
- assuming By acts upwards on CEB, the moments from By and F act in opposite directions around A.

Listing Ax, Ay, Bx, … etc., you have 12 unknowns, so to find them all you need 12 equations. Horizontal and vertical force balance on each L piece gives you 8 equations, so you will need four more from moment balance. Apply moment balance to some individual L pieces.

Since you are only asked for forces at A and B, you may be able to avoid finding all 12 by careful choice of which balance equations to use.

so how should I draw the FBD if I ignore the internal forces? I tried just the L for A and C and took Cx & Cy into account. then ACDG as one body and got F=0;

 

[haruspex]

so how should I draw the FBD if I ignore the internal forces? I tried just the L for A and C and took Cx & Cy into account. then ACDG as one body and got F=0;

In the diagram, F is applied to GE, so would not feature in any equation specific to ACDG.
Please post your equations.

 

[jojosg]

Member BE:

\sum F_x = 0 \quad \Rightarrow \quad \frac{F_G}{\sqrt{2}} = F + E_x

\sum F_y = 0 \quad \Rightarrow \quad E_y = \frac{F_G}{\sqrt{2}}

\Rightarrow F_G = \sqrt{2}E_y

From equilibrium: E_y = F + E_x



Member BC:

\sum F_x = 0 \quad \Rightarrow \quad B_x = E_x + \frac{F_C}{\sqrt{2}}

\sum F_y = 0 \quad \Rightarrow \quad B_y = E_y + \frac{F_C}{\sqrt{2}}

With substitution:

B_y = F + E_x + \frac{F_C}{\sqrt{2}}, \quad B_x = E_x + \frac{F_C}{\sqrt{2}}

Substituting E_y = F + E_x:

B_y = F + E_x + \frac{F_C}{\sqrt{2}}
B_x = E_x + \frac{F_C}{\sqrt{2}}



Joint B/Whole Structure:

\sum F_y = 0 \quad \Rightarrow \quad A_y + \frac{F_D}{2} + \frac{F_C}{2} = 0

\sum F_x = 0 \quad \Rightarrow \quad A_x + \frac{F_C}{2} + \frac{F_D}{2} = 0

Given A_y = A_x = 0:

\frac{F_G}{\sqrt{2}} - \frac{F_D}{\sqrt{2}} = 0, \quad \frac{F_G}{\sqrt{2}} = \frac{F_D}{\sqrt{2}}



Moment about B:

\sum M_B = 0 \quad \Rightarrow \quad -F(2a) = 0 \quad \Rightarrow \quad F = 0



Thus:

B_x = E_x + \frac{F_C}{\sqrt{2}}
B_y = E_x + \frac{F_C}{\sqrt{2}} \quad \text{(since } F = 0\text{)}

 

[haruspex]

I'll fix up your LaTeX by replacing each occurrence of [ tex ] and [ \ tex ] with a double #.
It is clearly not valid to conclude that F=0. Such a structure could be created and a force F applied and yet the structure resist movement.

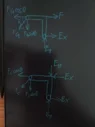
I am having trouble guessing what your labels for forces mean. Please state for each, what it acts on, at which point, and in what direction as positive.

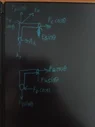
Member BE:
$\sum F_x = 0 \quad \Rightarrow \quad \frac{F_G}{\sqrt{2}} = F + E_x$

You've lost me already. By "member BE" do you mean the L shape from B to C via E? It'll be clearer to call that BC, since there is no label on the angle in DG or EG.
But if you do mean BC, F does not act directly on it.
What exactly is $F_G$? And why divide it by $\sqrt 2$?

$\sum F_y = 0 \quad \Rightarrow \quad E_y = \frac{F_G}{\sqrt{2}}$

$\Rightarrow F_G = \sqrt{2}E_y$

From this, it looks like you are defining $F_G$ as the total force DG exerts on EG and assuming, without justification, that it acts at 45° to the horizontal.

How about this notation for the forces:
At a junction J between two L shapes, $J_x$ and $-J_x$ are the horizontal forces they exert on each other, to the right being positive; $J_y$ and $-J_y$ are the vertical forces, up being positive. Adopt the convention that $J_x$ is the force the lower (lefthand) shape exerts on the upper (right hand) shape.
E.g. at E, BC exerts $E_x$ and $E_y$ on EG. It doesn’t matter if it turns out that BC pulls down on EG: that will simply produce a negative value for $E_y$.

I see no point in reading further till we get these issues sorted.

From equilibrium: $E_y = F + E_x$

Member BC:

$\sum F_x = 0 \quad \Rightarrow \quad B_x = E_x + \frac{F_C}{\sqrt{2}}$

$\sum F_y = 0 \quad \Rightarrow \quad B_y = E_y + \frac{F_C}{\sqrt{2}}$


With substitution:


$B_y = F + E_x + \frac{F_C}{\sqrt{2}}, \quad B_x = E_x + \frac{F_C}{\sqrt{2}}$


Substituting $E_y = F + E_x$:


$B_y = F + E_x + \frac{F_C}{\sqrt{2}}$


$B_x = E_x + \frac{F_C}{\sqrt{2}}$


Joint B/Whole Structure:


$\sum F_y = 0 \quad \Rightarrow \quad A_y + \frac{F_D}{2} + \frac{F_C}{2} = 0$


$\sum F_x = 0 \quad \Rightarrow \quad A_x + \frac{F_C}{2} + \frac{F_D}{2} = 0$


Given $A_y = A_x = 0$:


$\frac{F_G}{\sqrt{2}} - \frac{F_D}{\sqrt{2}} = 0, \quad \frac{F_G}{\sqrt{2}} = \frac{F_D}{\sqrt{2}}$


Moment about B:


$\sum M_B = 0 \quad \Rightarrow \quad -F(2a) = 0 \quad \Rightarrow \quad F = 0$


Thus:


$B_x = E_x + \frac{F_C}{\sqrt{2}}$


$B_y = E_x + \frac{F_C}{\sqrt{2}} \quad \text{(since } F = 0\text{)}$








Member BE:

$\sum F_x = 0 \quad \Rightarrow \quad \frac{F_G}{\sqrt{2}} = F + E_x$


$\sum F_y = 0 \quad \Rightarrow \quad E_y = \frac{F_G}{\sqrt{2}}$


$\Rightarrow F_G = \sqrt{2}E_y$


From equilibrium: $E_y = F + E_x$


Member BC:


$\sum F_x = 0 \quad \Rightarrow \quad B_x = E_x + \frac{F_C}{\sqrt{2}}$


$\sum F_y = 0 \quad \Rightarrow \quad B_y = E_y + \frac{F_C}{\sqrt{2}}$


With substitution:


$B_y = F + E_x + \frac{F_C}{\sqrt{2}}, \quad B_x = E_x + \frac{F_C}{\sqrt{2}}$


Substituting $E_y = F + E_x$:


$B_y = F + E_x + \frac{F_C}{\sqrt{2}}$


$B_x = E_x + \frac{F_C}{\sqrt{2}}$


Joint B/Whole Structure:


$\sum F_y = 0 \quad \Rightarrow \quad A_y + \frac{F_D}{2} + \frac{F_C}{2} = 0$


$\sum F_x = 0 \quad \Rightarrow \quad A_x + \frac{F_C}{2} + \frac{F_D}{2} = 0$


Given $A_y = A_x = 0$:


$\frac{F_G}{\sqrt{2}} - \frac{F_D}{\sqrt{2}} = 0, \quad \frac{F_G}{\sqrt{2}} = \frac{F_D}{\sqrt{2}}$


Moment about B:


$\sum M_B = 0 \quad \Rightarrow \quad -F(2a) = 0 \quad \Rightarrow \quad F = 0$


Thus:


$B_x = E_x + \frac{F_C}{\sqrt{2}}$


$B_y = E_x + \frac{F_C}{\sqrt{2}} \quad \text{(since } F = 0\text{)}$

 

[Lnewqban]

Member BE:
...
Member BC:
...
Joint B/Whole Structure:
...
Moment about B:
...

@jojosg
I would like to clarify that each of these L-shaped members work very differently than the members of a truss (like the one in your other thread).
These are rigid links which are able to transfer moments, besides compressing and tensioning forces.
For that reason, the pin connections resist forces that are that are induced by moments, besides forces that try to separate or crush them.
Those pin connections are unable to resist any moment (like any door's hinge).

The force F introduces a horizontal shear force to the whole structure.
An isolated GE member would simultaneously move to the right and rotate clockwise.
That movement is not occurring because the resistance to it from members BC and DG, via their pin connectors.
Members BC and DG are not moving or rotating either due to the resisting help of member AC and the solid ground.

External force F is reaching the ground while creating internal forces and moments in each of the members of this structure.
In the case of a truss, external forces acting on it are reaching the ground creating only internal compression and tension forces in its members and pin or roller connectors.

 

[tech99]

My ideas are as follows:-
If we are to ignore weights, the structure cannot be in equilibrium. So we must assign a weight W to the total structure and we have a centre of mass located on the vertical centre line. The structure acts exactly the same a a block of wood; you do not need to analyse twelve members, only the points at which forces are applied. Let the reactions at the supports be Av, Ah, Bv and Bh. The horizontal reaction is split equally between Ah and Bh. We cannot determine the split, so call it H.
Now analyse vertically, horizontally and then take moments about A (any point will work). This gives you 3 equations with 3 unknowns, which are Av, Bv and H.
When you have found H we have to assume an equal split of the horizontal reaction between Ah and Bh.

 

[haruspex]

My ideas are as follows:-
If we are to ignore weights, the structure cannot be in equilibrium.

Wrong.

 

[tech99]

Wrong.

I was assuming that the supports were knife edges so that the structure could lift off.

 

[brainpushups]

Not sure if this will confuse things, but perhaps approach the problem using the principle of virtual work? Was that taught as part of the course?

 

[haruspex]

I was assuming that the supports were knife edges so that the structure could lift off.

It says they are pin connected together. I agree the diagram is unclear though.

 

[Steve4Physics]

Isn’t the system statically indeterminate?

Considering only external forces, it is trivial to show that $A_y = - F, B_y = F$ and $A_x + B_x = -F$:

$A_x$ and $B_x$ cannot be uniquely determined because they have the same line of action. Consideration of the internal structure won't help. To illustrate this consider two extreme cases:

1. The pinned-support at B is replaced by a simple horizontal frictionless support; to provide the required upwards reaction. In this case the structure is in equilibrium with $B_x=0$ and $A_x = -F$.

2. Alternatively, the pinned-support at A is replaced by a rope pulling vertically downwards. In this case the structure is in equilibrium with $A_x=0$ and $B_x = -F$.

Or maybe I'm missing something?