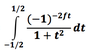Fourier Transforms: Solving Homework Problem 1/(1+t^2)

[tquiva]

Homework Statement

I am asked to find the Fourier transform of w(t)=1/(1+t^2)

Homework Equations

I know the only equations I need are:

The Attempt at a Solution

Therefore, I attempted the following:

I tried to expand the function in the integral and got:

I then tried to solve for this integral in terms of t from -1/2 to 1/2, and instead, the calculator says "Non-real result" and doesn't give me an answer. I know that exp(-ift)=cos(ft)+isin(ft) so the equation contains a complex part. But is there something else I need to do that I missed in my process? I even tried entering this integral into MatLab and still get the same answer as my Ti-89. I am now so frustrated.

Can someone please help me? I don't want to do a fft on Matlab or anything. I need to figure out this method. My assignment is due soon, so any help is greatly greatly appreciated. Thank you.

 

[I like Serena]

Your problem will be that a fractional power of (-1) is not defined in the real number domain.
You get a complex result.

 

[tquiva]

Your problem will be that a fractional power of (-1) is not defined in the real number domain.
You get a complex result.

I'm going from the time domain to the frequency domain, so the exponential must be negative right?
But still, I tried removing the negative sign... and the result remains the same. I get no answer, and the integral just stays as is. Any other ideas on what could be wrong? I'm using a Ti-89 calculator.

 

[I like Serena]

The exponential would still take on fractional values for an f between -(1/2) and +(1/2).

But either way, this integral is hard to evaluate and it does not become easier by changing the limits of the integral.
Can it be that you're supposed to look it up in a table of Fourier transforms?

 

[MisterX]

I don't know why you have the limits of integration as -1/2 and 1/2. Shouldn't they be -∞ and ∞?

Anyway, I was able to get the Fourier transform of 1/(1+t^2) using the Fourier Transform relationship for e^-a|t|, and using the duality principle.

 

[George Jones]

There is a more productive way to write

$$e^{-i2\pi ft}.$$