Free body diagrams, coordinate systems origin/orientation

[fog37]

Hello,
When solving statics or dynamics problems, one important step is to draw the free body diagram (FBD) with all the external forces acting ON the system. The "chosen" system may be composed of a single or multiple entities. The external forces have components that must be projects on the coordinate system which can be polar, Cartesian, etc.

My question is about the location of the origin $O$ and the orientation of the axes. In general, one rule of thumb is to place the origin $O$ where the point mass is or where the $CM$ of the system is. As far the system axes' orientation, it is mathematically convenient to align one of the axes with the net force direction. In this case, the axes are fixed in direction. In other situations, I have seen the origin $O$ being fixed at a specific spatial point with the two axes also fixed in direction.

The third option, which is also very common, is to choose a local coordinate system $O′x′y′$ with origin $O′$ centered on the particle and moving with the particle itself. It is effectively a local and moving Cartesian system. In the 2D case, one of the axis is parallel to the tangent to the trajectory and always aligned with the instantaneous velocity vector $\vec{v}(t)$ with the other axis is automatically perpendicular to the first axis. The acceleration vector $\vec{a}(t)$ is then decomposed into two components: the tangential component $a_{tan}$ and the radial or centripetal component $a_{centr}$.
Is this coordinate system choice $O'x'y'$ (local and moving with the particle, with one axis parallel to the direction of motion) always the most suitable and mathematically convenient choice? It looks like.

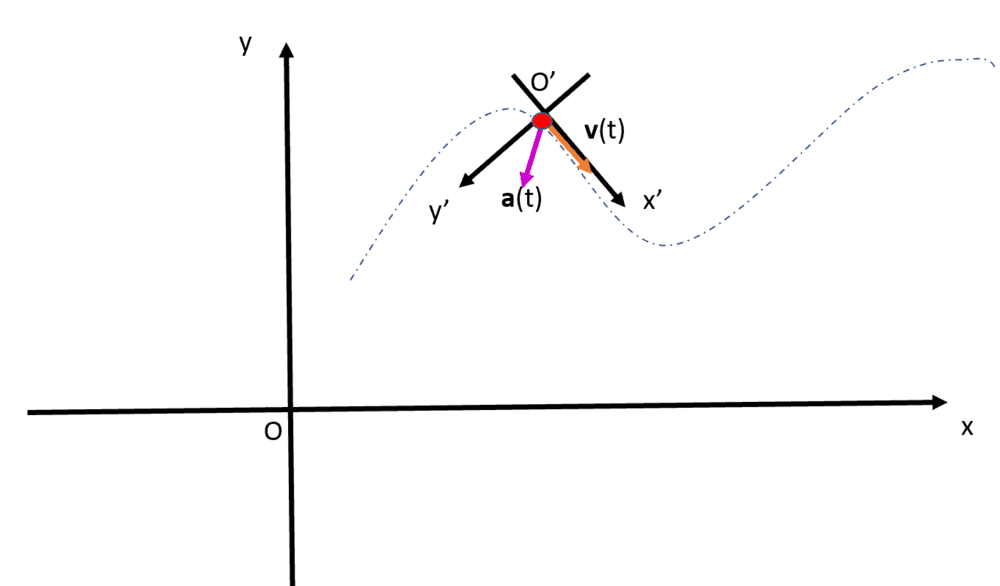
I struggle to see situations in which we would pick a coord. system $Oxy$ with origin $O$ not centered on the moving particle and with its axes in fixed directions instead of changing direction. It looks like the description of motion and the resolution of dynamics problems would be always more complicated.

On the other hand, the polar coordinate system has a fixed origin but its unit vectors change directions as the particle occupies different spatial positions...

Thanks!

 

[Dale]

Summary:: understand how to correctly use coord. systems when solving dynamics problems

Is this coordinate system choice O′x′y′ (local and moving with the particle, with one axis parallel to the direction of motion) always the most suitable and mathematically convenient choice?

No. In particular this coordinate system is non inertial. Often inertial coordinates are more convenient.

 

[fog37]

We always tend to use inertial systems because they only include and address only "real" forces, correct?
Noninertial systems always require real forces AND fictitious forces. When are noninertial systems useful then?

When solving basic dynamic problems involving rotation and centripetal force, the local coordinate system I describe above, with origin at the particle, is used but we don't include fictitious forces which means that the coord. system, at that moment and position in time, is not considered noninertial. I guess it is just the fixed Cartesian system conveniently positioned and oriented where the particle is. It is not a body-centered and moving coord. system then...

 

[etotheipi]

When are noninertial systems useful then?

I imagine it'd pretty useful if you want to play basketball on a merry-go-round

 

[Ibix]

When are noninertial systems useful then?

Naval gunnery is a textbook example. I believe there has been a recorded instance of a gunnery officer putting in the Coriolis effect with the wrong sign and therefore consistently missing the enemy.

 

[Dale]

Noninertial systems always require real forces AND fictitious forces. When are noninertial systems useful then?

Orbital mechanics is often done in non-inertial coordinates, as are weather models. Stress analysis for turbine blades. Magnetic resonance imaging. I am sure there are many more examples, those are the ones that come to mind for me.

 

[Vanadium 50]

I believe there has been a recorded instance of a gunnery officer putting in the Coriolis effect with the wrong sign and therefore consistently missing the enemy.

Legend is that this was the first Battle of the Falkland Islands, said to be the first major naval battle of the southern hemisphere. That part is not exactly true (Battle of Coronel was held at 38 degrees S five weeks earlier) and I have been unable to find any evidence for this outside of physics texts.

 

[Ibix]

I have been unable to find any evidence for this outside of physics texts.

Hm. I'm trying to track down where I read it - will let you know if I find it.

 

[Vanadium 50]

Thanks - if it helps, part of the legend is that the Germans had the right tables and the British the wrong ones, but they won anyway.

 

[Ibix]

I haven't found where I originally read it, but the Wikipedia talk page for the Battle of the Falkland Islands provides a quote from J.E. Littlewood (unsourced, but turns out to be p51 of A Mathematician's Miscellany), which cites personal communication with "an officer who was there" for a 100 yard miss and says this is about right. Littlewood provides no calculation and I haven't tried to work out what it might be.

 

[vanhees71]

We always tend to use inertial systems because they only include and address only "real" forces, correct?
Noninertial systems always require real forces AND fictitious forces. When are noninertial systems useful then?

One example is rigid-body motion, which leads to equations of motion that look much simpler in the body-fixed reference frame.

 

[A.T.]

When are noninertial systems useful then?

For example, when your boundary conditions are easier to describe in the non-inertial frame. Like movement along a rail that is fixed to a rotating platform.

 

[fog37]

I see. Thanks. So we can just introduce the fictious forces in case boundary conditions and/or are mathematically simpler in the noninertial frame.

I am thinking about orbital mechanics, moving planets and noninertial frames: why would it be easier to describe what is going on from the noninertial perspective of an observer on one of the rotating planets instead of from the perspective of an observer in an inertial system?

 

[Dale]

why would it be easier to describe what is going on from the noninertial perspective

I don’t know “why”, but have you ever tried to calculate the location of the Earth moon Lagrange points in an inertial frame?

 

[A.T.]

I am thinking about orbital mechanics,...

Try to calculate something specific, instead of just thinking about broad topics.