Free Vibration with Vicous Damping

[febbie22]

Hi, I am currently doing an experiment to determine the the viscous damping coefficient (c) of a dashpot.

Where you move the position of the damper to determine the effect of the damping

but my results show that when the damper is closer to the pivot the damping increases but i thought the futher away the damper is to the beam the more damping that gets put onto the beam.

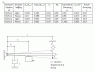
In the attachment is my result table and the figure that shows my experiment

any help would be great

Damper Positon(L2) Damper Setting Xm/Xm+1 In(Xm/Xm+1) Td Me (mass Equivalent) Equivalent Damping ce (L2/L)2 Actual Damping c (Nm/s)
50.5cm Light 1.156 0.145 0.36 4.05 3.26 0.472 6.91
50.5cm Heavy 1.33 0.288 0.34 4.05 6.86 0.472 15.5
18.3cm Light 1.031 0.031 0.34 4.05 0.74 0.062 11.9
18.3cm Heavy 1.12 0.113 0.34 4.05 2.70 0.062 43.55

Total length of beam is 73.5mm

 

[DaveC426913]

People are loath to open strange documents. Word docs can contain virii. You should post your findings so they are plainly readable.

 

[febbie22]

i was going to but the table of my results kept duffing up

 

[DaveC426913]

Use [ code ] tags:

50.5cm Light 1.156 0.145 0.36 4.05 3.26 0.472  6.91
50.5cm Heavy 1.33  0.288 0.34 4.05 6.86 0.472 15.5
18.3cm Light 1.031 0.031 0.34 4.05 0.74 0.062 11.9
18.3cm Heavy 1.12  0.113 0.34 4.05 2.70 0.062 43.55

or upload a screen capture.


BTW, is this homework? It should be entered using the homework templates.

 

[AlephZero]

The measured data makes sense. The four values of X_m/X_{m+1} look reasonable and they say the vibration was more damped when the damper is further from the pivot.

You haven't said how you calculated the rest of your numbers and came to the opposite conclusion.

 

[febbie22]

Thanks for the reply here's my sample calculation

Position 1 – 50.5 cm Damper Setting – Light

Offset on graph is 1.979mm

The offset of the graphs have to be added to the peaks

Xm = 0.751 + 1.979 = 2.73 mm Xm+1 = 0.379 + 1.979 = 2.358 mm

Xm / Xm+1 = 2.73/2.358 = 1.156

In(Xm/Xm+1) = In(1.156) = 0.145

Td = T2 – T1 = 7.16 – 6.8 = 0.36

L1 = 0.352m L = 0.735m M = 0.7 kg m = 2.1kg

Me = M.(L1/L)² + m/3 = 7 x (0.352/0.735)² + 2.1/3 = 2.31 kg

In(Xm/Xm+1) = (Ce x Td) / (2 x Me)

ce = (In(Xm/Xm+1) x (2 x Me)) / Td

ce = (0.145 x 4.61) / 0.36 = 1.86

( L2/L)² = (0.505/0.735)2 = 0.472

c = ce / 0.472 = 3.26 /0.472 = 3.93 Ns/m

i just noticed that i calculated Me wrong fixed now

 

[febbie22]

When i calculate (L₂/L)² for damper position 2 18.3cm i get 0.062 which means that when i divde that with the equivalent damping coefficient i get a bigger damping (c)

 

[AlephZero]

What are T1 and T2?

Are you measuring the spring stiffness by measuring the position of the beam with and without the extra mass, or something like that?

 

[febbie22]

T1 and T2 is the time periods of two successive peaks taking from my graphs that show the oscillation to get the T_d period of the damped oscillation.

The spring stiffness wasn't needed to calculate the damping constant

 

[AlephZero]

T1 and T2 is the time periods of two successive peaks taking from my graphs that show the oscillation to get the T_d period of the damped oscillation.

OK, understood.

The spring stiffness wasn't needed to calculate the damping constant

Well, you need two out of three from K, M, and Td, but it doesn't matter which two.

I don't have time to work through this right now, but I'll be back...

 

[febbie22]

thanks for the help much appreciated

 

[AlephZero]

I think you have got in a tangle about exactly what quantities you are calculating, so let's go through the first case.

In mass normalized modal coordinates, the equation of motion is
\ddot\xi + 2 \beta \omega \dot\xi + \omega^2 \xi = 0

The damped oscillation solution is
\xi = e^{-\beta\omega t} e^{i\omega_D t}
where \omega_D^2 = \omega^2(1 - \beta^2).

You have the period = 0.36s and the amplitude ratio = 1.156
Assume \omega and \omega_D are near enough equal since the damping is small.
\omega_D = 2 \pi / 0.36 = 17.45 rad/s

For one complete cycle, \omega t = 2 \pi
So e^{-2 \pi \beta} = 1/1.156
\beta = (\ln1.156) / 2 \pi ) = 0.0231

So the modal damping coefficient = 0.0231.

To convert the equation of motion into physical (SI) units measured at the end of the beam, we need to multiply everything by the effective mass = 2.31 kg

So if the damper was at the end of the beam, the equaton of motion would be
2.31 \ddot x + (2.31)(2)(0.0231)(17.45) \dot x + (2.31)(17.45) x = 0
So if it was at the end of the beam the force in the dashpot would be 1.86 Ns/m

But the velocity in the actual dashpot is lower by a factor of .505/.735 = 0.687
So the force in the actual dashpot is (1.86)(0.735)/0.505 = 2.71 Ns/m

Now repeat this for the 3rd case

\omega_D = 2 \pi / 0.34 = 19.63 rad/s
\beta = (\ln1.031) / 2\pi = 0.00432
Equivalent dashpot at end of beam = (2.31)(2)(0.00432)(19.63) = 0.392 Ns/m
Dashpot at actual position = (0.392)(0.735)/(0.183) = 1.57 Ns/m

OK, 1.57 and 2.71 are not very close, but measuring small amounts of damping accurately is not easy.

For the heavy damping cases, I get 6.00 Ns/m and 6.56 Ns/m.
The difference is about 10%, which is probably as good as you are likely to get from this sort of experiment.

 

[febbie22]

Thank you very much Aleph

 

[febbie22]

Aleph i actually got the vaule for the heavy postion 2 it is actually 1.062 which makes the overall damping about 3 which is about 50% off of the light.

im not sure why its not working.