Frequency of oscillating cylinder

[LiorE]

Homework Statement

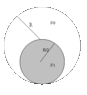
The problem is this: Find the angular frequency of the system in the figure when it's displaced at a small angle from equlibrium, given that ρ_0 < ρ_1. There is friction with the ground, so the motion is a rolling motion, without slipping.

Homework Equations

I used the following equations, and got a wrong answer:

f_s = friction
m = mass of small cylinder
M = mass of large cylinder
x = linear displacement from equilibrium
θ - angular displacement from equilibrium

for linear forces (here the tag stands for d/dt):

f_s = (m+M)x''

since it's a rolling motion:

x = Rθ
so: x'' = Rθ''

And the equation for the moments, from the center of the large cylinder (I think this is wrong):

f_sR - mgsinθ*R/2 = Iθ''

also:

m = (π ρ_1 R^2)/4
M = π ρ_0 R^2 - (π ρ_0 R^2)/4
I = π ρ_0 R^4 - (π ρ_0 R^4)/2 + (π ρ_1 R^4)/2

The Attempt at a Solution

Using all the above equations and getting the ODE for x gives (unless I got the factors wrong):

ω = (ρ_1/(10ρ_0 + 6ρ_1))*(g/R)

This is not right - the right answer is:

ω = (10(ρ_1 - ρ_0)/(7(ρ_1 + 31ρ_0))*(g/R)

Which is of course a lot more sensible since there shouldn't be an oscillation for ρ_1 = ρ_0, and for ρ_1 < ρ_0 the model is wrong.

So what's the right answer? And what am I doing wrong?

Thanks,

Lior

BTW - why isn't the latex working?

 

[LiorE]

Oh, the figure...

4 characters

 

[LiorE]

And also -

ρ_0, ρ_1 are the mass densities of the respective parts of the cylinder.