Frictionless Force question

aliciaw0 · Aug 4, 2005

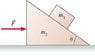
Find an expression for the magnitude of the horizontal force F in the figure for which m1 does not slip either up or down along the wedge. All surfaces are frictionless.

since it has nothing to do with the friction i am thinking that m1 and the force have to have the same acceleration in the horizontal direction for it not to slide up or down, but im not sure what to do from there?

thanks

abercrombiems02 · Aug 5, 2005

Ok this is what i recommend you do. Setup and FBD for the smaller block alone. You should get your sum of forces vectically to equal zero. The horizontal sum of forces on the smaller block must equal its mass multiplied by its acceleration (F=ma). You know the blocks must accelerate together so acc_block = acc_system. Now apply sum(Fext) = m_sys*a_sys.

aliciaw0 · Aug 5, 2005

thanks i tried what you told me too and i think i still might have done it wrong?

f(block1)y: Fn-Fgcos(theta)=0

F(block1)x: Fgsin(theta)=m1a Fgsin(theta)/m1= a

system x: F= (m1+m2) ((m1g*sin(theta)/m1) and they said my answer was wrong because it doesnt depend on theta. so if you know where to go from here it would be helpful! thanksss

Doc Al · Aug 5, 2005

aliciaw0 said:

f(block1)y: Fn-Fgcos(theta)=0

F(block1)x: Fgsin(theta)=m1a

The acceleration of the smaller block is purely horizontal, so define your components accordingly. Let the x-axis be horizontal, not down the plane; let the y-axis be vertical, not perpendicular to the plane.

Redo these two equations. The normal force will have both vertical and horizontal components. The weight should be set equal to [itex]m_1 g[/itex].

aliciaw0 · Aug 6, 2005

yay i got it right thankkk you

Y: Fn= (m1*g)/cos(theta)

X: (m1*g*tan(theta))/m1 = a

system: F= (m1+m2) ((m1*g*tan(theta))/m1 ) =]

Log in or Sign up

Frictionless Force question

aliciaw0

Attached Files:

phy.jpg

abercrombiems02

aliciaw0

Doc Al

Staff: Mentor

aliciaw0