Function Growing Exponentially then Constant at X=0?

  • Context: Undergrad 
  • Thread starter Thread starter germangb
  • Start date Start date
  • Tags Tags
    Function
Click For Summary

Discussion Overview

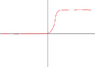
The discussion revolves around identifying a mathematical function that exhibits exponential growth as it approaches X=0 and then remains constant at a certain Y value. The scope includes theoretical exploration of function properties and potential examples.

Discussion Character

  • Exploratory, Technical explanation, Conceptual clarification

Main Points Raised

  • One participant describes a function that grows exponentially at X=0 and then becomes constant, seeking examples of such a function.
  • Another participant suggests that this could relate to functions that are ##\mathcal C^\infty## but not analytic, referencing concepts from Differential Geometry.
  • A participant proposes that the logistic function may fit this description, providing a link to its Wikipedia page.
  • Another participant mentions the sigmoid function as a possible candidate, also linking to its Wikipedia page.
  • One participant suggests the error function as another potential example.
  • A different perspective is offered regarding the unit step response of a damped harmonic oscillator, noting its oscillatory behavior at high points.
  • A participant shares the mathematical representation of the sigmoid function.

Areas of Agreement / Disagreement

Participants present multiple competing views on what functions may satisfy the described behavior, with no consensus reached on a single function or model.

Contextual Notes

Some contributions reference specific mathematical properties and types of functions, but there are no settled definitions or agreements on the exact nature of the function in question.

germangb
Messages
7
Reaction score
0
I have this function representation whch grows exponentially when it reaches X=0, but then it remains constant at some Y

does anybody know a function which looks like that?
 

Attachments

  • Sin título.png
    Sin título.png
    800 bytes · Views: 494
Last edited:
Mathematics news on Phys.org
As an example of ##\mathcal C^\infty## but not analytic? As a way to glue ##\mathcal C^\infty##-ly? Such a function is usually explained in Differential Geometry books in a section title Partitions of Unity.
 
germangb said:
I have this function representation whch grows exponentially when it reaches X=0, but then it remains constant at some Y

does anybody know a function which looks like that?
Looks like a logistic function to me. See http://en.wikipedia.org/wiki/Logistic_function.
 
Logistic Function.
 
Unit step response of a damped harmonic oscillator? (It seems to oscillate a bit at its high point)
 
thank you all very much :biggrin:
 
Sigmoid:

y = \frac{1}{1+e^{-x}}
 

Similar threads

Undergrad Looking for S-shaped function with range 0 to 1 (but not asymptotic)
  • · Replies 3 ·
Replies
3
Views
1K
Graduate Fitness function for window length of filter
  • · Replies 1 ·
Replies
1
Views
1K
Undergrad My attempt to understand horizontal transformations of functions
  • · Replies 6 ·
Replies
6
Views
2K
High School Exponential Growth: Modeling growth in months vs years
  • · Replies 3 ·
Replies
3
Views
4K
MHB Rules for Finding the Base of a Exponential Function?
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Alternating Harmonic Numbers are cool, spread the word!
  • · Replies 4 ·
Replies
4
Views
3K
Undergrad Plotting polar equations and scale invariance
  • · Replies 7 ·
Replies
7
Views
2K
High School Understanding exponentiation and logarithms together
  • · Replies 12 ·
Replies
12
Views
2K
High School What is the notation for denoting constants in a function?
  • · Replies 2 ·
Replies
2
Views
1K
Is ##f(x)=2^{x}-1## considered an exponential function?
  • · Replies 12 ·
Replies
12
Views
3K