Function riding on another function

  • Thread starter preposterous
  • Start date
  • Tags
    Function
In summary, to write sin(x) along a half circle, you can use the function f1 = 0.1*sin(x) with the x-axis being f2 = sqrt(10^2 - x^2). This may not pass the vertical line test, but for certain applications, such as when the amplitude of sin(x) is small compared to the circle radius, it can be used. Another way to express this is in polar coordinates, where r = 1 + 0.5*cos(theta), and in Cartesian coordinates, the relationship r^2 = x^2 + y^2 and tan(theta) = y/x can be used. Another option would be to use 0.1 * sin(sqrt(10
  • #1
preposterous
3
0
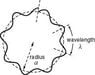
How do I write sin(x) where the x-axis is a function itself. For example, I want to write sin(x) along a half circle. I need to "wrap" the function, similar to "De Broglie wavelength" in image below.

More specifically, I want to write f1 = 0.1*sin(x) the where the x-axis is f2 = sqrt(10^2 - x^2).

I know that this generally will not pass the vertical line test. But for my application it will becuase the sin(x) has small amplitude compared to the circle radius.
 

Attachments

  • deBroglie_E.jpg
    deBroglie_E.jpg
    5.9 KB · Views: 452
Mathematics news on Phys.org
  • #2
Hey preposterous.

One example like the diagram in your post would be in polar co-ordinates:

r = 1 + 0.5*cos(theta)

where in cartesian co-ordinates you use the relationship:

r^2 = x^2 + y^2 and

tan(theta) = y/x
 
  • #3
Why not

0.1 * sin(sqrt(10^2 - x^2))
 

FAQ: Function riding on another function

What is "Function riding on another function"?

"Function riding on another function" refers to the concept of one function using another function as its input or output. This allows for more complex and dynamic programming, as the output of one function can be fed directly into another function.

What is the difference between a main function and a sub-function?

A main function is the primary function that is called by the program, while a sub-function is a function that is called by the main function. Sub-functions are used to break down complex tasks into smaller, more manageable steps.

How do you define a function riding on another function in programming?

In programming, a function riding on another function is defined by using the output of one function as the input for another function. This can be achieved by passing the first function as an argument to the second function, or by nesting the second function within the first function.

What are the advantages of using function riding on another function?

Using function riding on another function allows for more modular and reusable code. It also makes it easier to debug and maintain code, as changes can be made to individual functions without affecting the overall program.

What are some common use cases for function riding on another function?

Function riding on another function is commonly used in web development for tasks such as data manipulation, form validation, and event handling. It is also used in scientific and mathematical programming for tasks such as graphing and data analysis.

Similar threads

B Looking for a specific periodic function
Replies
4
Views
1K
I How do I do this calculation involving the SIN function?
Replies
9
Views
1K
I Best fit to an oscillating function
Replies
9
Views
2K
I Best way to fit three functions
Replies
2
Views
915
I Alternating Harmonic Numbers are cool, spread the word!
Replies
4
Views
1K
A Finding Minimal Mean Distance Curves on the Unit Sphere
Replies
2
Views
1K
I Geometry and algebraic equations
Replies
4
Views
1K
MHB Couple of hard trig questions....
Replies
1
Views
1K
A Converting this vector into polar form
Replies
4
Views
2K
I Normalized Angular Rotation/Position Equations?
Replies
3
Views
1K

Hot Threads

Recent Insights

Back
Top