dynamicskillingme
- 26
- 0
Homework Statement
For a gauge function G(t,q) where
does
stevendaryl said:Oh, so you're just talking about Lagrangian mechanics.
If G is a function of q and t, then you have:
\dot{G} = \frac{\partial G}{\partial q} \dot{q} + \frac{\partial G}{\partial t}
So in that case, \frac{\partial \dot{G}}{\partial \dot{q}} = \frac{\partial G}{\partial q}
dynamicskillingme said:A quick question about the same function, wouldbe a true statement?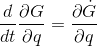
stevendaryl said:Yes, if G is only a function of q and t.
dynamicskillingme said:G is a function of q and t, (G(t,q) to be exact). Could you explain why you can change the order of the derivatives in this case?