tylerscott
- 28
- 0
Hello,
I am currently working on a problem to calculate the light that makes it through a half circle. For example, say I put a cylinder out in the sun, where the intensity is known to be 1030 W/m^2. I would like to compute the intensity/energy/power that makes it into this. Now, given the curvature of this half circle, I know this will somehow need to incorporate an integration over the sphere based upon the angle, but I'm thinking I'm missing some fundamental physics equation in the process.
See attached picture for the idea I have in my mind.
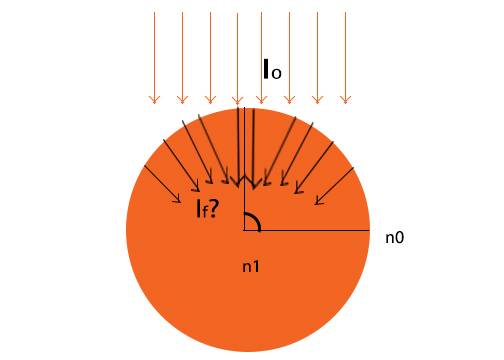
I am currently working on a problem to calculate the light that makes it through a half circle. For example, say I put a cylinder out in the sun, where the intensity is known to be 1030 W/m^2. I would like to compute the intensity/energy/power that makes it into this. Now, given the curvature of this half circle, I know this will somehow need to incorporate an integration over the sphere based upon the angle, but I'm thinking I'm missing some fundamental physics equation in the process.
See attached picture for the idea I have in my mind.