General relativity - Using Ricc and Weyl tensor to find the area

[edoofir]

Homework Statement

General relaivity, Geodesic equation

Relevant Equations

General relativity equations

I have the following question to solve:Use the metric:$$ds^2 = -dt^2 +dx^2 +2a^2(t)dxdy + dy^2 +dz^2$$

Test bodies are arranged in a circle on the metric at rest at $t=0$.
The circle define as $$x^2 +y^2 \leq R^2$$

The bodies start to move on geodesic when we have $$a(0)=0$$

a. we have to calculate the second derivative of the area of the circle $$S = \int{\sqrt{g^(2)}dxdy}$$ respected to time and express your answer using the Ricci tensor.

b. calculate the second derivative respected to time of the ratio of the diagonals $$D_1, D_2$$ and express it using Weyl tensor.

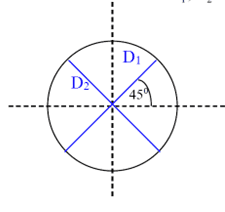
I have already solved section a and now I would like to get some help/ideas how can I solve section b. I had an idea using the geodesic deviation equation but I am not sure how can I use it in here.

Thanks for the ones who will try to help me :)

 

[anuttarasammyak]

I observe for $D_1$
dl^2=2(1+a^2)dx^2
and for $D_2$
dl^2=2(1-a^2)dx^2