Solving Geodesics with Metric $$ds^2$$

[edoofir]

I have the following question to solve:Use the metric:
$$ds^2 = -dt^2 +dx^2 +2a^2(t)dxdy + dy^2 +dz^2$$

Test bodies are arranged in a circle on the metric at rest at $$t=0$$.
The circle define as $$x^2 +y^2 \leq R^2$$

The bodies start to move on geodesic when we have $$a(0)=0$$

a. we have to calculate the second derivative of the area of the circle $$S = \int{\sqrt{g^(2)}dxdy}$$ respected to time and express your answer using the Ricci tensor.

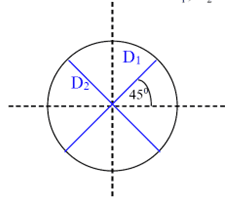
b. calculate the second derivative respected to time of the ratio of the diagonals $D_1$ and $D_2$ and express it using Weyl tensor.

The Christoffel symbols:
$$ \Gamma^{t}_{xy} = \Gamma^{t}_{yx} = a(t)a'(t)$$
$$\Gamma^{x}_{tx} = \Gamma^{x}_{xt} = \frac{a^3(t)a'(t)}{a^4(t)-1} $$
$$\Gamma^{y}_{ty} = \Gamma^{y}_{yt} = \frac{a^3(t)a'(t)}{a^4(t)-1} $$
$$\Gamma^{x}_{ty} = \Gamma^{x}_{yt} = \frac{a(t)a'(t)}{1-a^4(t)} $$
$$\Gamma^{y}_{tx} = \Gamma^{y}_{xt} = \frac{a(t)a'(t)}{1-a^4(t)} $$

the Ricci tensors:

$$R_{tt} = \frac{2a^2(2a'^2 -aa''(a^4-1))}{(a^4-1)^2}$$
$$R_{xx} = R_{yy} = \frac{2a^2a'^2}{a^4-1}$$
$$R_{xy}=R_{yx} = a'^2 +aa''$$where $$a = a(t), a' = \frac{da}{dt}, a'' = \frac{d^2a}{dt}$$

and i calculated the second derivative of the area of the circle:
$$ \frac{ds^2}{dt^2} = \int{[\frac{d^2}{dt^2}\sqrt{1-a^4}dxdy + 2\frac{d}{dt}\sqrt{1-a^4}(\frac{dx}{dt}dy + dx\frac{dy}{dt})+\sqrt{1-a^4}(\frac{d^2x}{dt^2}dy+\frac{dx}{dt}\frac{dy}{dt}+dx\frac{d^2y}{dt^2})]} $$
I am not sure what should i do next. any suggestions?

 

[Ibix]

You seem to have some sign errors in $\Gamma^x_{ty}$ and $\Gamma^y_{tx}$.

I'm not sure how you got that expression for $d^2S/dt^2$. What's your expression for $S$? And what is the Ricci tensor and the geodesics followed by the test particles?

 

[edoofir]

thank you for your reply.
I have calculated the Christoffel symbols using Mathmatica. are you sure there is a sign error? isn't it that: $$\Gamma^{y}_{ty} = \Gamma^{y}_{yt}$$?

If it's not the case i will try to calculate agin but it according to Mathmatica it should be the signs (else i don't understand what you ment).
Second, the expression for $S$ is: $$S = \int{\sqrt{g^(2)}dxdy}$$ as i mentiond.

 

[Ibix]

Yes, the signs were just an overall sign that you lost - just a typo it seems, fine.

How are you getting from that expression for $S$ to the second derivative of area, was what I wanted to know. I was hoping you would show a few steps in the derivation.

 

[edoofir]

i attach here the calculation in the photos.

This is how i understood to take the second derivative respected to time. I understood that dx and dy are also being effected.

I also show there the Geodesic equations i have calculated using the Christoffel symbols.
can you please explain what overall sign i lost in the Christoffel symbols?

 

[Ibix]

I'll double check my Christoffel symbols.

The problem with your approach to the derivative of the area is that I think the limits of integration are time dependant, so you need to carry out the integral before computing the derivative, I think.

 

[Ibix]

Rechecked my Christoffel symbols and you are correct - apologies. I missed that you'd taken the minus sign into the denominator.

 

[edoofir]

Thank you very much for responding. i am not sure i understood what you are saying about the derivative of the area. I carry the integral all the way.
the integration of the integral should be:
for y: $$ -\sqrt{R^2-x^2}<y<\sqrt{R^2-x^2}$$
and for x: $$-R<x<R$$

That's how i understad it so farm, so what do you mean by saying they are time dependant?

 

[Ibix]

i am not sure i understood what you are saying about the derivative of the area.

The point is that $R$ depends on $t$, so I don't think $\frac{d^2}{dt^2}\int\sqrt{g^{(2)}}dxdy$ is the same as $\int\frac{d^2}{dt^2}\sqrt{g^{(2)}}dxdy$.

In any case, do you have an expression for $R(t)$?

 

[edoofir]

I understood it is not the same, this is why I used the derivation of a product rule and got the expression i got. (I attached a photo of how i got it).

Yes, i have expression for the Ricci tensors (if that's what you mean):

$$R_{tt} = \frac{2a^2(2a'^2 -aa''(a^4-1))}{(a^4-1)^2}$$
$$R_{xx} = R_{yy} = \frac{2a^2a'^2}{a^4-1}$$
$$R_{xy}=R_{yx} = a'^2 +aa''$$where $$a = a(t), a' = \frac{da}{dt}, a'' = \frac{d^2a}{dt}$$

 

[Ibix]

I'm struggling to read your screenshots on my phone. Deriving the geodesic equations myself, I now think that the particles do not change coordinates, so their positions always satisfy $x^2+y^2=R^2$ where $R$ is an arbitrary constant, nothing to do with any tensor.

I think you are supposed to be calculating the second derivative of the area enclosed by the ring of test particles, which is the region defined as $x^2+y^2\leq R^2$. I don't understand why you don't do this integral directly - neither $a$ nor $R$ is a function of $x$ or $y$ so it looks to me to be trivial. Then you can simply differentiate; I assume this will lead you to something that looks like the Ricci scalar.