RCopernicus
- 23
- 1
We've all seen an image similar to this one:
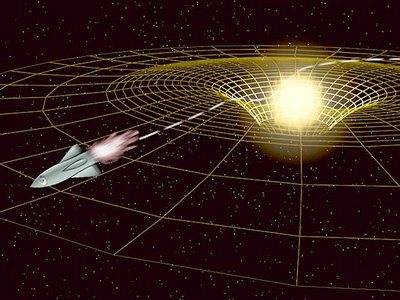
This is displaying the projection of GR Geodesics onto 3-D space (well, 2D in the picture). I'm still working my way through the General Relativity texts, so I'm not yet able to do the calculation on my own. Can anyone give me a formula that I can poke into a simulation that takes the mass an input parameter and gives me the geodesic coordinate system projected onto the 2-D space? I'm basically looking to draw the concentric circles in the above picture (given a mass).
This is displaying the projection of GR Geodesics onto 3-D space (well, 2D in the picture). I'm still working my way through the General Relativity texts, so I'm not yet able to do the calculation on my own. Can anyone give me a formula that I can poke into a simulation that takes the mass an input parameter and gives me the geodesic coordinate system projected onto the 2-D space? I'm basically looking to draw the concentric circles in the above picture (given a mass).