Geometric Sets and Tangent Subspaces - McInnerney, Example 3

[Math Amateur]

I am reading Andrew McInerney's book: First Steps in Differential Geometry: Riemannian, Contact, Symplectic ...

I am currently focussed on Chapter 3: Advanced Calculus ... and in particular I am studying Section 3.3 Geometric Sets and Subspaces of $T_p ( \mathbb{R}^n )$ ...

I need help with a basic aspect of Example 3.3.7 ...

Example 3.3.7 reads as follows:

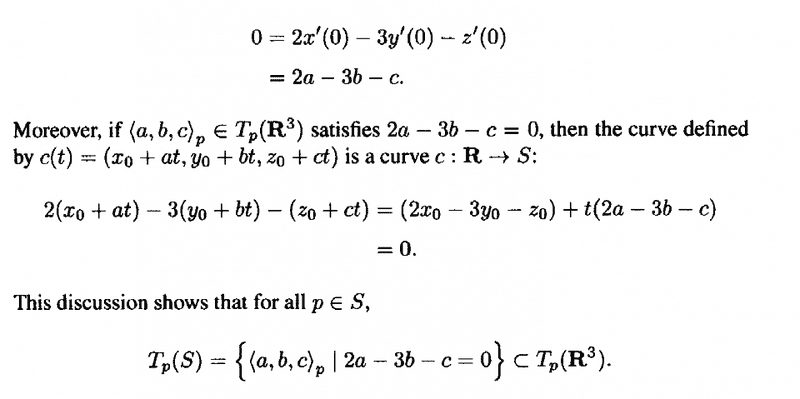
Question 1

In the above text we read:

" ... ... Let $p = ( x_0, y_0, z_0 ) \in S$ i.e. $2 x_0 - 3 y_0 - z_0 = 0$. ... ... "... BUT ... as I read the example ... ... we have that $2 x_0 - 3 y_0 - z_0 = 0$ is the equation of $c(t)$ at $( x_0, y_0, z_0 )$ ... AND ... again as I see it ... this is not all of $S$ as $c$ maps $I$ into $S$ ... thus a general point $p = ( x_0, y_0, z_0 ) \in S$ may not satisfy the equation as it may not be in the range of $c$ ...Can some please clarify my issue with the example... ? (I hope I have made my question clear ..)===========================================================

*** EDIT ***

After some reflection I now feel that all points in $S = \phi (U) = ( u, v, 2u - 3v )$ satisfy the equation $2x - 3y - z = 0$ ... so a particular point $p = ( x_0, y_0, z_0)$ obviously satisfies $2x_0 - 3y_0 - z_0 = 0$ ... is that right ... ?

Please let me know if my edit is correct ...
==========================================================


Question 2

In the above text we read:

" ... ... This discussion shows that for all $p \in S$,

$T_p (S) = \{ (a, b, c)_p \ \ | \ \ 2a - 3b - c = 0 \} \subset T_p ( \mathbb{R}^3 )$

... ... ... ... "Now, it seems that vectors at $p = (x_0, y_0, z_0)$ that have components $a, b, c$ respectively which obey the equation, $2a - 3b - c =0$ are (I think?) in $S$ ... ... so this would mean that $T_p(S)$ is a subset of $S$ ... Is that correct ...?Question 3

Does anyone know of any books with a simple approach to tangent spaces replete with a number of worked/computational exercises ...?
Hope someone can help with the above questions ...

PeterI have made a simple diagram of my understanding of the mappings involved ... as follows ... ...

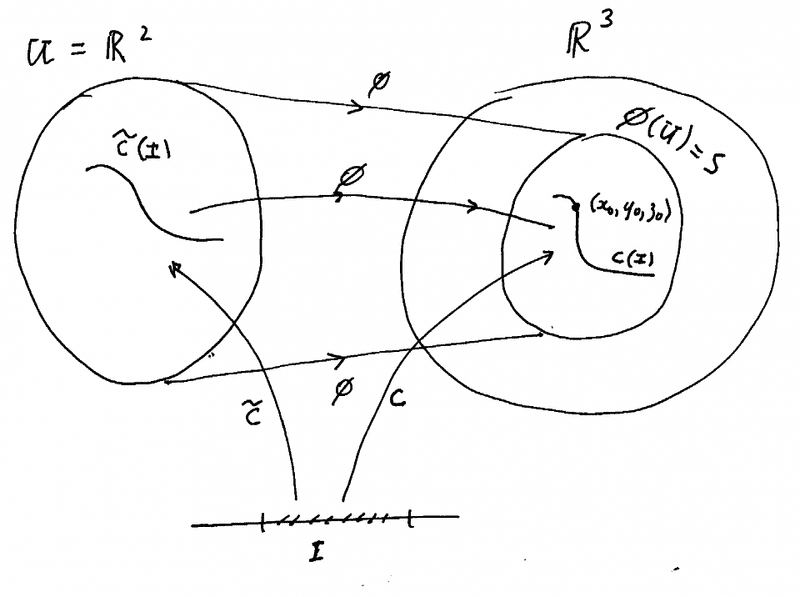Is the above diagram a correct representation of the mappings involved?
To help to give some of the context and some explanation of the theory and notation relevant to the above I am providing McInerney's introduction to Section 3.3 as follows:

 

[andrewkirk]

*** EDIT ***

After some reflection I now feel that all points in $S = \phi (U) = ( u, v, 2u - 3v )$ satisfy the equation $2x - 3y - z = 0$ ... so a particular point $p = ( x_0, y_0, z_0)$ obviously satisfies $2x_0 - 3y_0 - z_0 = 0$ ... is that right ... ?

Please let me know if my edit is correct ..

Yes, it is correct.

Question 2

In the above text we read:

" ... ... This discussion shows that for all $p \in S$,

$T_p (S) = \{ (a, b, c)_p \ \ | \ \ 2a - 3b - c = 0 \} \subset T_p ( \mathbb{R}^3 )$

... ... ... ... "Now, it seems that vectors at $p = (x_0, y_0, z_0)$ that have components $a, b, c$ respectively which obey the equation, $2a - 3b - c =0$ are (I think?) in $S$ ... ... so this would mean that $T_p(S)$ is a subset of $S$ ... Is that correct ...?

No. A vector in the tangent space $T_pS$ is not in the space $S$ itself, because the former holds both location and direction information, whereas the latter holds only location information. It's like the difference between 'going through Paris in a Northerly direction at 50 km/h' and just 'Paris'.

You can think of the former as a vector of six components, with the first three giving location and the second three giving velocity (direction and magnitude), and the latter as a vector of only three components, giving just location.

 

[Math Amateur]

Thanks for the help Andrew ... but just a clarification ...

We know that $S = \phi (U) = (u, v, 2u - 3v)$

So points in $S$ satisfy $2x - 3y - z$... this is the equation that vectors in $T_P (S)$ must satisfy ... so surely all the points of the vector $< a, b, c >_p$ lie in $S$ ...

I understand that the points of $S$ do not have a direction and that points are conceptually different from vectors in that vectors have magnitude and direction and points do not ... but can't we say that the points of the vector $< a, b, c >_p$ lie in $S$ ... ?

Peter

 

[andrewkirk]

$2x - 3y - z =0$... this is the equation that vectors in $T_P (S)$ must satisfy

Remember that the vector in $T_pS$ is a 6-tuple $<a,b,c,x,y,z>$ (a '6-vector') with the first three components indicating mag and direction and the second three indicating location. What we can say in this case, and only because the plane $S$ passes through the origin, is that both $<x,y,z>$ and $<a,b,c>$, regarded as '3-vectors', must satisfy the equation. So you can think of each of those two as being in $S$, but neither is the 6-vector, because each contains only half of the information content of the 6-vector.

An element of $T_pS$ is a 6-vector, which in this case we can think of two 3-vectors, while an element of $S$ is just a 3-vector.

Note also that while $<x,y,z>$ and $<a,b,c>$, interpreted as points in Euclidean 3-space, lie in the same plane S, they do not necessarily point in the same direction. Consider the vector $<-2,3,-13>_{<3,2,0>}$ which is the vector at point $<3,2,0>$ pointing in direction $<-2,3,-13>$, and has 6-tuple representation $<-2,3,-13,3,2,0>$. The direction in which the 3-vector is pointing is (if I've done my calcs right) perpendicular to the location 3-vector whose tail is at the origin and head is at $<3,2,0>$. But both 3-vectors lie in the plane $S$.

Another way to visualize vectors in $T_pS$ is as signposts showing the direction and distance to another city. Consider a signpost in Glasgow pointing along a Roman road ('cos they're straight) to Edinburgh that says 'Edinburgh 100km'. The direction of the signpost and the distance 100km is the $<a,b,c>$ info of the 6-vector. The location of the signpost (eg its latitude and longitude) is the $<x,y,z>$ info of the 6-vector.

 

[Math Amateur]

Remember that the vector in $T_pS$ is a 6-tuple $<a,b,c,x,y,z>$ (a '6-vector') with the first three components indicating mag and direction and the second three indicating location. What we can say in this case, and only because the plane $S$ passes through the origin, is that both $<x,y,z>$ and $<a,b,c>$, regarded as '3-vectors', must satisfy the equation. So you can think of each of those two as being in $S$, but neither is the 6-vector, because each contains only half of the information content of the 6-vector.

An element of $T_pS$ is a 6-vector, which in this case we can think of two 3-vectors, while an element of $S$ is just a 3-vector.

Note also that while $<x,y,z>$ and $<a,b,c>$, interpreted as points in Euclidean 3-space, lie in the same plane S, they do not necessarily point in the same direction. Consider the vector $<-2,3,-13>_{<3,2,0>}$ which is the vector at point $<3,2,0>$ pointing in direction $<-2,3,-13>$, and has 6-tuple representation $<-2,3,-13,3,2,0>$. The direction in which the 3-vector is pointing is (if I've done my calcs right) perpendicular to the location 3-vector whose tail is at the origin and head is at $<3,2,0>$. But both 3-vectors lie in the plane $S$.

Another way to visualize vectors in $T_pS$ is as signposts showing the direction and distance to another city. Consider a signpost in Glasgow pointing along a Roman road ('cos they're straight) to Edinburgh that says 'Edinburgh 100km'. The direction of the signpost and the distance 100km is the $<a,b,c>$ info of the 6-vector. The location of the signpost (eg its latitude and longitude) is the $<x,y,z>$ info of the 6-vector.

Thanks for the help, Andrew ... appreciate it

Still reflecting on what you have said ...

Do you know a good and preferably basic reference that treats tangent spaces at undergrad level ... and has some worked examples ,,,

Peter