- #1
Дьявол
- 365
- 0
Hi! I am trying to find out where:
[tex]cos\theta=\frac{a \cdot b}{|a||b|}[/tex]
came from.
Here is mine geometrical interpretation of scalar projection:
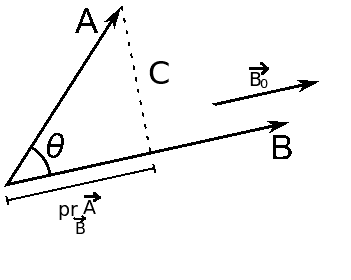
Now, (pr means projection)
[tex]pr_{\overrightarrow{A}} \overrightarrow{B} = p\overrightarrow{B_0}[/tex]
and
[tex]cos\theta=\frac{|pr_{\overrightarrow{A}} \overrightarrow{B}|}{|A|}[/tex]
[tex]cos\theta=\frac{|pB_0|}{|A|}=\frac{|p|}{|A|}[/tex]
How do
[tex]cos\theta=\frac{a_xb_x+a_yb_y+a_zb_z}{|a||b|}[/tex]
for 3 dimensional coordinate system, wher |a| and |b| are modulo of "a" and "b" ?
Thanks in advance.
Regards.
[tex]cos\theta=\frac{a \cdot b}{|a||b|}[/tex]
came from.
Here is mine geometrical interpretation of scalar projection:
Now, (pr means projection)
[tex]pr_{\overrightarrow{A}} \overrightarrow{B} = p\overrightarrow{B_0}[/tex]
and
[tex]cos\theta=\frac{|pr_{\overrightarrow{A}} \overrightarrow{B}|}{|A|}[/tex]
[tex]cos\theta=\frac{|pB_0|}{|A|}=\frac{|p|}{|A|}[/tex]
How do
[tex]cos\theta=\frac{a_xb_x+a_yb_y+a_zb_z}{|a||b|}[/tex]
for 3 dimensional coordinate system, wher |a| and |b| are modulo of "a" and "b" ?
Thanks in advance.
Regards.